R 语言功能强大,探索性数据分析(EDA),统计分析模型,数据挖掘模型,数据可视化,样样精通。报告方面有媲美Jupyter Notebook的RMarkdown,使用knit和pandoc生成,颜值颇高。交互方面有shiny,也有让人惊艳的效果。
但是硬伤就是语言本身的可读性不高(基本每次写都要参考别人的代码,某些语法样式也很奇怪,不是天天用很难记得住),并且过度依赖IDE(RStudio)。当然,命令行或者自带的GUI也是可以使用的,但就是不好用啊。所以对于较复杂的程序,例如较复杂的爬虫,文本处理以及特化的数据清洗等,R 使用起来就有诸多不便,并且运行性能也是数一数二的低。
所以仅仅使用 R 来进行 EDA,做一些较简单的数据清洗,模型训练和可视化,是一个较明智的选择。尤其是涉及统计学分析或者金融的时序分析的时候,用起来顺手。下面简单复习一下统计分析中的常用操作。
基础功能
1. 矩阵的生成
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 生成数组序列
x <- 1:6
# 使用 array 生成指定维度的矩阵
X <- array(x, dim=c(2,3))
# 使用 matrix 生成指定维度的矩阵
Xr <- matrix(x, nrow=2, ncol=3, byrow=TRUE)
# 按行合并矩阵
Cr <- rbind(X, Xr)
# 按列合并矩阵
Cc <- cbind(X, Xr)
# 生成对角矩阵
diag(3)
diag(3, nrow=2, ncol=3)
2. 矩阵运算
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 元素和
X + Xr
# 元素积
X * Xr
# 转置
Xr <- t(Xr)
# 矩阵乘法
X %*% Xr
# 逆矩阵
solve(X[1:2, 1:2])
# 对应行列式的值
det(X[,-3])
# 求特征值和特征向量
eigen(X[,-3])
# 奇异值分解
svd(X[,-3])
3. 统计分析常用函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 基本
# min/max/mean/median/rank/quantile/sd/var/cov/cor/
# sum/length/range/sort/order/sample
# 统计概要
summary(X)
# Min. 1st Qu. Median Mean 3rd Qu. Max.
# 2.00 3.25 4.50 4.50 5.75 7.00
# apply,按列计算均值
apply(X, MARGIN=2, FUN=mean)
# 排列组合
# choose/factorial
# 概率分布
###########################################
# 概率分布 # 函数名 # 概率分布 # 函数名
# beta分布 beta # 对数正态分布 lnorm
# 二项分布 binom # 逻辑分布 logis
# 柯西分布 cauchy # 负二项分布 nbinom
# 卡方分布 chisq # 正态分布 norm
# 指数分布 exp # 泊松分布 pois
# F分布 f # T分布 t
# 伽马分布 gamma # 均匀分布 unif
# 几何分布 geom. # 韦布尔分布 weibull
#超几何分布 hyper #
###########################################
# 区间估计与假设检验
# t.test() -- 单正态总体和两正态总体的均值的t检验
# var.test() -- 单正态总体和两正态总体的方差的F检验
# chisq.test() -- 列联表和拟合优度的卡方检验
4. 可视化分析
R-base绘图语句分三层:
- 高层函数创建一个新图形,包括坐标轴、标签、标题等;
- 低层函数在已有图形上添加更多信息,如额外的点、线、标签;
- 交互函数允许用户通过光标向已有图形交互地增加信息,或者从中释放信息。
1
2
3
4
5
6
# 打开一个绘图窗口
windows()
# 划分绘图窗口
par(mfrow=c(2, 2))
# 绘图
plot(1:10, 1:10)
高层函数的用法:
plot(x, y):如果x,y是数值向量,生成y对x的散点图;- plot(x, y):如果x是一个因子对象,y是一个数值向量,生成y对应于x各个水平的箱形图;
plot(X):如果X是包含两个变量的列表或者一个两列(x和y)的矩阵,生成y对x的散点图;- plot(X):如果X是一个时间序列,生成一个时序图;
- plot(X):如果X是一个复向量,生成虚部对实部的散点图;
- plot(X):如果X是一个因子对象,生成x的条形图。
好吧,内置的plot函数的用法是有点奇葩,但是用习惯了还挺好用。它的本意应该是让我们在做EDA的时候,不管什么数据都可以plot一下。不管那么多,plot了再说。其他常用函数:
pairs(X):如果X是数值矩阵或者数据框,生成一个配对的散点图矩阵,矩阵由X中每列的列变量对其他各列列变量的散点图组成,即两两互相作为自变量和因变量。coplot(a~b|c):括号里面没有转义字符,就是输进去的参数!a,b为数值向量,c是数值向量或者因子对象。相当于多了个分类变量,三维数据绘图。qqnorm(y=1:1000):正态分位数-分位数图qqplot(x, y):y 对 x的分位数-分位数图hist(c(1:10, 12)):直方图- …
低层函数用法:
points(2, 1):添加点lines(c(2, 4, 6, 8), c(1, 2, 0, 1)):添加线text(10, 1, "strings"):在特定点添加文本abline(1, 0.2):添加一条纵截距为1,斜率为0.2的直线abline(h=0.2):添加一条高度为0.2的水平线abline(v=3.5):添加一条位于3.5的垂直线polygon(c(1,2,3,4,3,2,1), c(1,2,3,4,5,6,1)):绘制一个多边形,顶点由x,y指定legend():添加图例,具体见下面例子axis():在当前图形的指定边上添加坐标text(1, 1, expression(paste(bgroup("(", atop(n,x), ")"), p^x,q^{n-x}))):添加数学公式
5. 绘图例子
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 自变量
x <- seq(-pi, pi, len=65)
# 正弦曲线
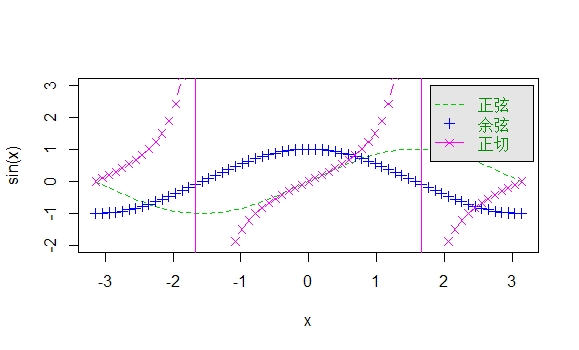
plot(x, sin(x), type="l", ylim=c(-2,3), col=3, lty=2)
# 添加余弦散点
points(x, cos(x), col=4, pch=3)
# 添加正切曲线
lines(x, tan(x), type="b", lty=1, pch=4, col=6)
# 添加图例
legend(
x=1.8, y=3, legend=c("正弦","余弦","正切"),
col=c(3, 4, 6),
text.col="green4",
lty=c(2, -1, 1),
pch=c(-1, 3, 4),
bg='gray90'
)
统计分析例子
1. 计算相关系数
1
2
3
4
5
6
7
8
r_coef <- function(a, b){
# 输入:a、b两个数组
# 输出:a与b的相关系数
rss1 <- sum( (a-mean(b)) * (b-mean(b)) )^2
rss2 <- sum( (a-mean(a))^2 ) * sum( (b-mean(b))^2 )
r <- rss1 / rss2
return(r)
}
2. 总体均值置信区间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
E.con.interval <- function(x, sig, a, fun){
# x -- 所要提供的样本
# sig -- 标准差;当 sig 未知,需要定义为:FALSE
# a -- 风险值,显著性水平,对应的置信度为(1-a)
# fun -- 对应的分布,可分为两种情况:
# 1)正态分布 -- fun="norm";条件为:(满足大样本 n>=30 | 正态总体且 sig 已知)
# 2)t分布 -- fun="t";条件为:(总体正态 & sig未知 & 小样本)
# 控制精度
k <- seq(-5, 5, 0.001)
# 不同分布对应的统计量 Z
if(fun == "norm"){
z <- mean(pnorm(k) <= (a/2)) * 10 - 5
}else{
z <- mean(pt(k, df=length(x)-1) <= (a/2)) * 10 - 5
}
# 若总体标准差未知则使用样本标准差代替
if (sig == FALSE) {
sig <- sqrt(sum((x-mean(x))^2) / (length(x)-1))
}
# 标准化的逆过程,得到总体均值的置信临界值以及对应得置信区间
u1 <- mean(x) - z * sig / sqrt(length(x))
u2 <- mean(x) + z * sig / sqrt(length(x))
return(c(u1, u2))
}
3. 总体方差置信区间
1
2
3
4
5
6
7
8
9
10
11
12
13
sig.con.interval<-function(x,a){
# 类似上例,这里只考虑正态总体的情况
# x:观测序列
# a:显著性水平
k <- seq(0, 50, 0.001)
z1 <- mean(pchisq(k, length(x)-1) <= (a/2))*50
z2 <- mean(pchisq(k, length(x)-1) <= (1-a/2))*50
d1 <- (length(x)-1)*sd(x)^2 / z1
d2 <- (length(x)-1)*sd(x)^2 / z2
return(c(d1,d2))
}
4. 最小二乘线性回归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
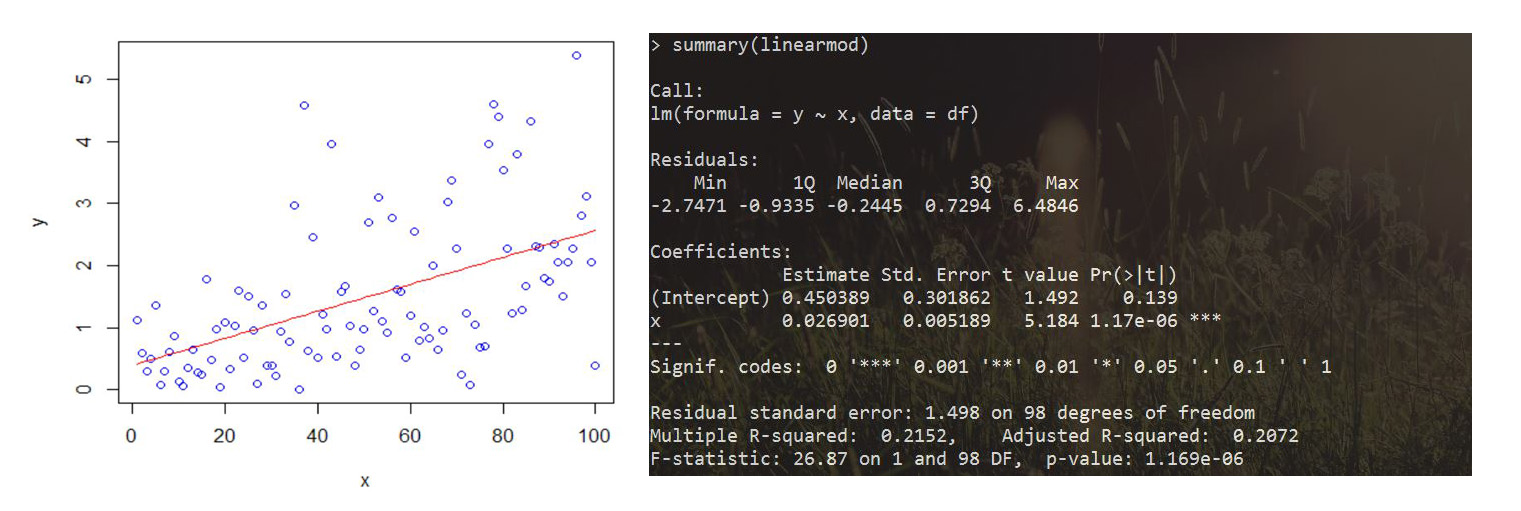
"A example of linear regression and some details of OLS"
# Generate random data and add a linear tendency
x <- 1:100
y <- abs(rnorm(100)) # 正态随机样本
y[34:66] <- y[34:66] * 2 # 线性趋势
y[67:99] <- y[67:99] * 3
df <- data.frame(x=x, y=y)
plot(x, y, col='blue')
# Fit model
linearmod <- lm(y~x, data = df) # OLS模型拟合
y_pred <- predict(linearmod) # 训练集预测
points(x, y_pred, type='l', col='red')
# Compute statistics
SST <- sum((y-mean(y))^2) # 样本总变异
SSE <- sum((y_pred-mean(y))^2) # 解释平方和
SSR <- sum((y-y_pred)^2) # 残差平方和
R_quared <- SSE / SST # 拟合优度
# Details
summary(linearmod)