R 机器学习 统计分析 编程语言 数据分析 笔记 RCM

R 统计学习（ISLR）-- Learning Notes (I)

统计学习简介 | 线性回归 | 分类问题

Posted by Paradise on January 10, 2021

Python 解决方案：https://github.com/hardikkamboj/An-Introduction-to-Statistical-Learning

教材介绍：https://book.douban.com/subject/26430936/

相关资源：http://faculty.marshall.usc.edu/gareth-james/ISL/

第一章 导论

  • 1.1 统计学习概述
  • 1.2 统计学习历史
  • 1.3 关于这本书
  • 1.4 本书适合的读者群
  • 1.5 记号与简单矩阵代数
  • 1.6 本书的内容安排
    • 第 2 章主要介绍统计学习的基本技术和概念，包含 K 最邻近算法
    • 第 3、4 章是经典的线性回归模型和分类模型（线性回归、logistic 回归、线性判别）
    • 第 5 章介绍交叉验证和自助法
    • 第 6 章提供了一类集经典与现代与一体的线性模型，这些方法是在标准线性回归基础上的改进（逐步变量选择、岭回归、主成分分析、偏最小二乘法和 lasso ）
    • 第 7 章介绍一类在一元输入问题中颇有成效的非线性方法，之后应用到多输入模型
    • 第 8 章介绍树类模型，包括挂袋法、提升法、随机森林
    • 第 9 章介绍支持向量机
    • 第 10 章介绍聚类，重点介绍主成分分析、K-means 聚类和系统聚类方法。
  • 1.7 用于实验和习题的数据集

第二章 统计学习

2.1 什么是统计学习

用 f 表示自变量和因变量的函数关系，统计学习就是估计 f 的一系列方法。

  • 2.1.1 什么时候需要估计 f
    • 估计 f 的主要原因有两个：预测（prediction）和推断（inference）
    • 预测：求函数对应关系 f，一般情况下 f 视为“黑箱”，即不关心 f 的具体形式，只关心准确地预测。其精确性依赖于可约误差和不可约误差。
  • 2.1.2 如何估计 f
    • 可分为参数方法和非参数方法
    • 参数方法：建立模型，使用训练数据集去拟合（fit）或训练（train）模型，获得 f 的参数，比如最小二乘法拟合参数。
    • 非参数方法：不需要对函数形式事先做明确的假设，估计函数在平滑处理后尽可能与更多的数据点接近。
  • 2.1.3 预测精度和模型解释性的权衡
    • 预测越精确，模型越复杂，自变量越多，模型解释性越弱。
  • 2.1.4 指导学习与无指导学习
    • 半指导学习：一部分观测点可以同时观测到预测变量和响应变量，一部分观测不到响应变量。
  • 2.1.5 回归与分类问题
    • 将被解释变量为定量数据的问题称为回归分析问题，对应定性的为分类问题。

2.2 评价模型精度

  • 2.2.1 拟合效果检验
    • 在回归中常用的标准为 MSE（均方误差），选择的模型应该使测试数据集的 MSE 尽可能小
    • 在分类问题中的标准为错误率（误差比率，误差观测点的占比）
    • 实践中可能缺乏测试集，代替方案是使训练均方误差（tarin MSE）尽可能小，缺点是可能出现过拟合（亦即光滑度过高）
    • 上问题的对应解决方案称作交叉验证
  • 2.2.2 偏差-方差的权衡
    • 在数学上，训练 MSE 的期望可以表达为 y_hat 的方差、y_hat 偏差的平方和误差项 error 的方差三者之和。因此存在这个权衡。
    • 一般而言，使用光滑度更高的方法所得的模型方差会增加，偏差会减小。这两个量相对的变化率影响 MSE 的大小。
  • 2.2.3 分类模型
    • 一个好的分类器应使错误率尽可能小
    • 贝叶斯分类器：可以在数学上证明测试错误率存在最小值。平均来说，可以设计一个简单的分类器将每个观测值分配到它最可能在的类别中。这种方法称作贝叶斯分类器
    • 贝叶斯边界：划分不同类别归纳的边界
    • 贝叶斯分类器将产生最低的测试错误率，称为贝叶斯错误率
    • K 最邻近方法（KNN）：使用贝叶斯方法需要知道给定 X 后 Y 的条件分布，在现实中很难获取。许多方法尝试在给定 X 后估计 Y 的条件分布，如 K 最邻近法
    • KNN 分类器原理：首先识别训练集的 K 个最靠近 x0 的点集，用 N0 表示。然后对每个类别 j 分别用 N0 中的点估计一个分值作为条件概率的估计。然后再运用贝叶斯规则将测试观测值 x0 分到概率最大的类中
    • 正如回归设置中，训练错误率和测试错误率没有必然关系。一般而言，当使用光滑度更高的方法（K 值更小，决策边界更曲折），训练错误率将减小，但是测试错误率不定。随着 1/K 的增大，测试错误率的变化近似 U 型

2.3 实验：R 语言简介

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

# 查看环境中所有创建的对象
ls()
# 创建一个数值矩阵
x <- matrix(data = c(1,2,3,4), nrow = 2, ncol = 2)
x <- matrix(c(1,2,3,4), 2, 2, byrow = TRUE)
# 正态分布随机变量(标准正态分布)
x <- rnorm(100, mean = 0, sd=1)
y <- rnorm(100, mean = 50, sd=.1)
# 相关系数
cor(x, y)
# 方差和标准差
var(y)
sd(y)
sqrt(var(y))
# 希望代码每次运行产生一样的随机数组
set.seed(213)	# 参数为任意整数
mean(rnorm(100))

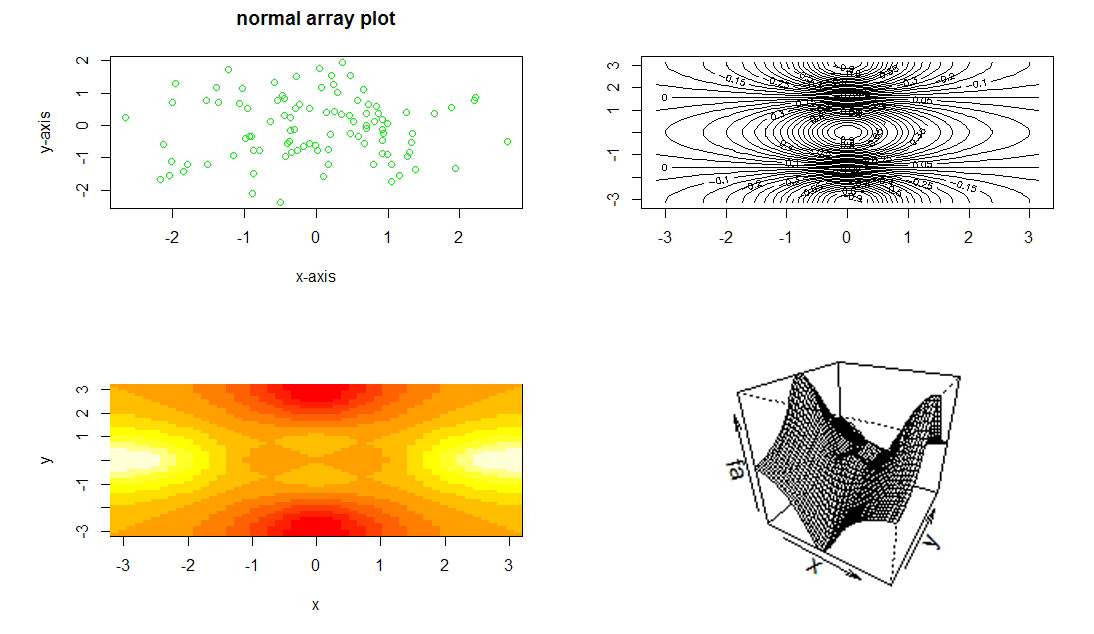
#绘图基础
x <- rnorm(100)
y <- rnorm(100)
plot(x, y, col='green',
     xlab = 'x-axis', ylab = 'y-axis', main = 'normal array plot')
# 保存图片
pdf('figure.pdf')
dev.off()

# 使用 contour() 函数产生一个等高线图
x <- seq(-pi, pi, length.out = 50)
y <- x
f <- outer(x, y, function(x,y) cos(y) / (1+x^2))
contour(x, y, f)
fa <- (f-t(f)) / 2
contour(x, y, f, nlevels = 45, add = T)
#使用image()函数生成热力图
image(x, y, fa)
persp(x, y, fa, theta = 30, phi = 30)


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

# 索引数据
A <- matrix(1:16, 4, 4)
dim(A)
A[1, 4]
A[c(1,2), c(1,2)]
A[1:3, 1:3]
A[1:2, ]
A[-c(1,2), ]
A[-c(1,2), -c(3,4)]

# 载入数据
library(ISLR)
# 写入时默认编码为UTF-8
write.table(Auto, 'Auto.csv', sep = ',', quote = FALSE, row.names = FALSE)
Auto2 <- read.csv('Auto.csv')
# 打开可视化的交互式编辑器
fix(Auto)
# 剔除包含缺失值的行
Auto <- na.omit(Auto)
# 查看数据
dim(Auto)
names(Auto)

# 将内置数据储存到环境变量
attach(Auto)
# 将定量数据转换成定性数据
cylinders <- as.factor(cylinders)		# 这时多了一个levels属性
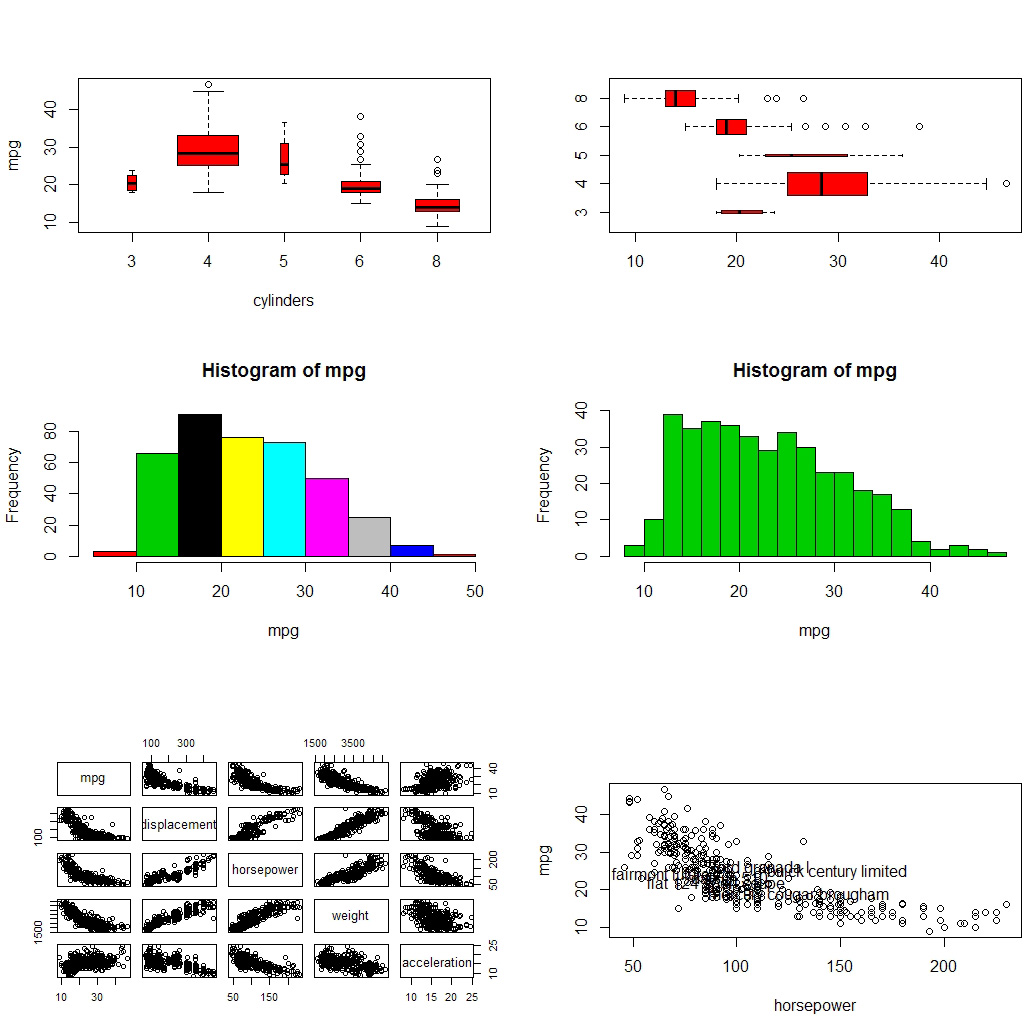
# 对定性数据可以直接plot产生箱形图
plot(cylinders, mpg, col='red', varwidth=TRUE, xlab='cylinders', ylab='mpg')
plot(cylinders, mpg, col='red', varwidth=TRUE, horizontal=TRUE)
# 绘制直方图
hist(mpg, col = sample(1:8))			# 共有8种颜色
hist(mpg, col = 3, breaks = 15)

#散点图矩阵
pairs(Auto)
#指定变量绘制散点图矩阵
pairs(~mpg+displacement+horsepower+weight+acceleration, Auto)

#紧随绘图之后使用identify函数进行交互式看图
plot(horsepower, mpg)
identify(horsepower, mpg, name)
#输出统计信息
summary(Auto)

第三章 线性回归

回顾线性回归模型的主要思路以及常用的最小二乘法

3.1 简单线性回归

  • 3.1.1 估计系数
    • 残差平方和：RSS = sum(residual^2)
    • 最小二乘法估计参数：
      • beta1_hat = sum((x-mean(x)) * (y-mean(y)) / sum((x-mean(x))^2)
      • beta2_hat = mean(y)- beta1_hat * mean(x)
  • 3.1.2 评估系数估计值的准确性
    • 复习计量和统计中讨论的无偏性、置信区间、假设检验以及 P 值等问题
  • 3.1.3 评价模型的准确性
    • 使用参数：残差标准误 RSE 和拟合度 R^2

3.2 多元线性回归

  • 3.2.1 估计回归系数
    • 同样使用最小二乘法，最小化 RSS
  • 3.2.2 一些重要问题
    • 响应变量和预测变量之间是否有关系？– F 检验
    • 如何选定重要变量？– 通过 F 检验获得的 P 值选择
    • 如何衡量模型拟合度？– 常用 RSE 和 R^2

3.3 回归模型中的其他注意事项

  • 3.3.1 定性预测变量
  • 3.3.2 线性模型的扩展
  • 3.3.3 潜在的问题
    • 非线性的响应-预测关系
    • 误差项的自相关
    • 误差项异方差性
    • 离群点
    • 高杠杆点（类似离群点）
    • 共线性

3.4 营销策划（例子）

3.5 线性回归与K最邻近法的比较

  • KNN 更灵活，但是缺少解释性，而且存在维数灾难

3.6 实验：线性回归

线性回归分析

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# 导入库
librarY(ISLR)
library(MASS)

# 在数据编辑窗口打开 data.frame
fix(Boston)
# 在编辑器窗口打开
view(Boston)
# 查看 filed 和 document
names(Boston)
?Boston

# 简单线性模型
mod <- lm(medv~lstat, data=Boston)
# 查看模型参数
print(mod)
names(mod)
summary(mod)
view(broom::glance(mod))

# 系数估计值的置信区间
confint(mod)
# 计算置信区间和预测区间
predict(mod, data.frame(lstat=(c(5,10,15))), interval = 'confidence')
predict(mod, data.frame(lstat=(c(5,10,15))), interval = 'prediction')

# 绘制残差散点图
plot(predict(mod), residuals(mod))
# 学生化残差
plot(predict(mod), rstudent(mod))
# 残差表明数据存在一定的非线性,计算杠杆统计量
plot(hatvalues(mod))
#具有最大杠杆统计量的值
which.max(hatvalues(mod))

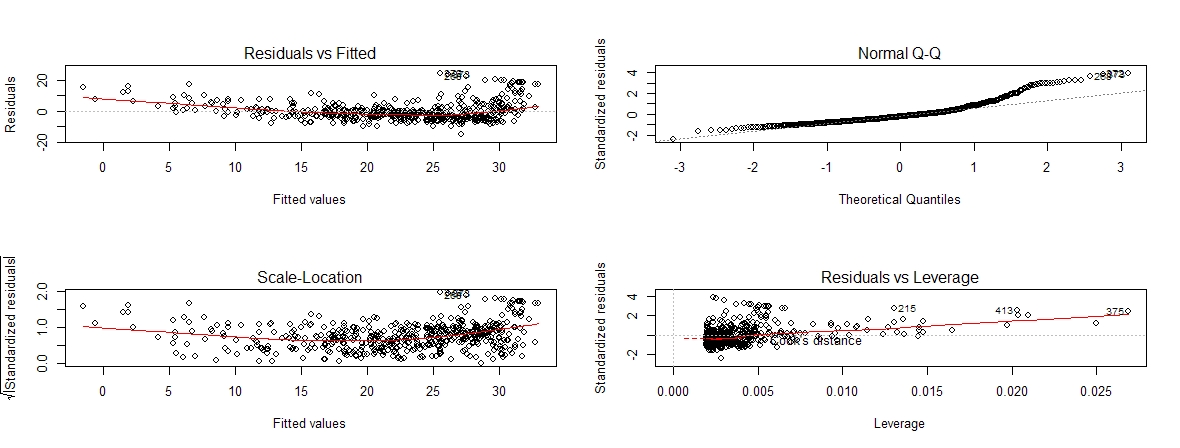
# 模型诊断图
par(mfrow=c(2,2))
plot(mod)


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 在线性回归中引入交互项
lm(medv~lstat*age, data = Boston)    # 相当于medv~lstat+age+lstat:age

# 对预测变量进行非线性变化
mod1 <- lm(medv~lstat, data = Boston)
mod2 <- lm(medv~lstat+I(lstat^2), data = Boston)
summary(mod1)
summary(mod2)

#可以看到加入二次项后P值接近于0
#进一步量化二次拟合在何种程度上优于线性拟合
===============================================================
> anova(mod1,mod2)
Analysis of Variance Table

Model 1: medv ~ lstat
Model 2: medv ~ lstat + I(lstat^2)
  Res.Df   RSS Df Sum of Sq     F    Pr(>F)    
1    504 19472                                 
2    503 15347  1    4125.1 135.2 < 2.2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
===============================================================

# 可视化二次模型，可以看到残差中可识别规律更少，即拟合效果更好 
par(mfrow=c(2, 2))
plot(mod2)

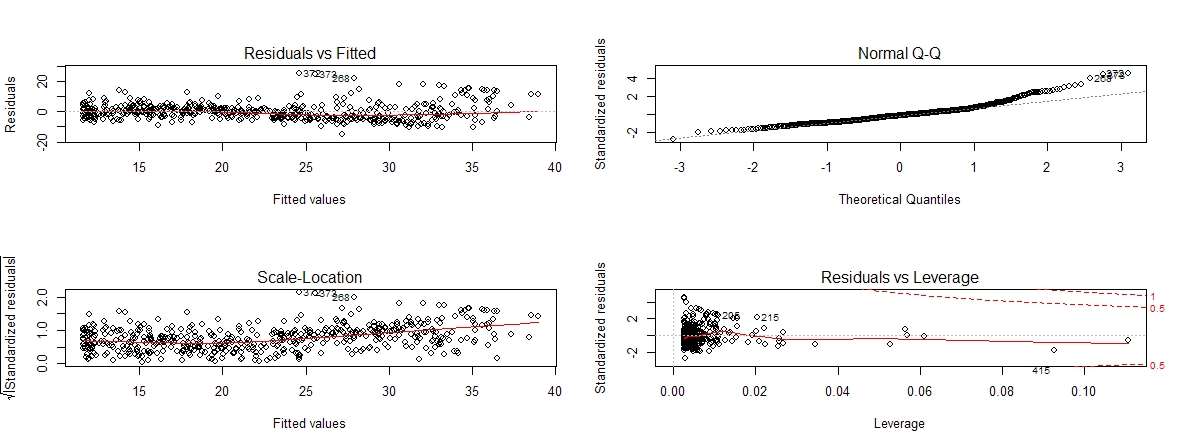
加入非线性变量

1
2
3
4
5
6
7
8
9
10
11
12
13

# 创建更高阶多项式拟合
mod5 <- lm(medv~poly(lstat,5), data = Boston)	# 使用poly生成5阶多项式
summary(mod5)

# 进行对数变换
log_mod <- lm(medv~log(rm), data = Boston)
summary(log_mod) 

# 由于对数化后还是单调递增的，可以sort一下方便画成曲线
points(sort(Boston$rm), sort(predict(log_mod)), col='red', type='l', lwd=3)
bools <- residuals(log_mod) < 0
points(Boston$rm, residuals(log_mod), col='red', type = 'h')
points(Boston$rm[bools], residuals(log_mod)[bools], col='green', type = 'h')

第四章 分类

  • 响应变量为定量变量的问题为回归，对应定性变量的问题的分类
  • 应用最广泛的三种分类模型：
    • 逻辑斯蒂回归（logistic regression）
    • 线性判别分析（linear discriminant）
    • K 最邻近（K-nearest neighbor）

4.1 分类问题概述

4.2 为何线性回归不可用

  • 为什么不直接用二值化的虚拟变量代表响应变量？比如将某个三类分类问题经过编码给每一类分别赋值为 1、2、3？
  • 这样做实际上默认了一个有序的输出，默认第 2 类到第 1、3 类的差距是一样的。因为有顺序性，不同的编码实际上会产生一个不同的回归模型。
  • 注意到如果是两类变量可以直接使用二值化线性回归（哑变量方法）。同时，如果多类问题中，各类别确实有相应的顺序关系，那么也可以通过编码进行线性回归。

4.3 逻辑斯蒂回归

  • 4.3.1 逻辑斯蒂模型
    • 模型基本形式：p(X) = beta0 + beta1*X，其中：p(X) = P(Y=1|X)
    • 存在的问题是拟合出来的 Y 预测值可能出现负值，因此使用逻辑斯蒂函数进行“归一化”：
      • p(X) = e^(beta0 + beta1*X) / [1 - e^(beta0 + bata1*X)]
    • 相关的术语：发生比（odd）、对数发生比（log-odd）、分对数（logit）
  • 4.3.2 估计回归系数
    • 由于 beta 参数未知，因此需要训练数据对参数进行估计。可以使用最小二乘法进行估计，但是极大似然方法有更好的估计效果。
  • 4.3.3 预测
  • 4.3.4 多元 logistic 回归
    • 模型形式的扩展与多元线性模型类似
  • 4.3.5 响应分类数大于 2 的 logistic 回归
    • 虽然二元的 logistic 回归可以扩展到多类问题，但是实践中不常用

4.4 线性判别分析（linear discriminant analysis, LDA）

  • logistic 回归建立了直接估计 p(Y=k | X=x) 的模型，而线性判别分析则是分别对每种响应分类建立预测变量 X 的分布模型，再利用贝叶斯定理反过来去估计 p(Y|X)
  • 当分布接近正态分布，线性判别分析模型在形式上与 logistic 模型相似
  • 为何需要使用线性判别分析方法：
    • 当类别区分度较高时，logistic 模型估计的参数不够稳定；
    • 当样本量较小，而且每一类响应分类中对应得 X 接近正态分布时，线性判别分析模型更加稳定；
    • 应用到多类别分类时，使用线性判别分析模型。
  • 4.4.1 运用贝叶斯定理进行分类
  • 4.4.2 p=1 的线性判别分析
  • 4.4.3 p>1 的线性判别分析
  • 4.4.4 二次判别分析（quadratic discriminant analysis, QDA）

4.5 分类方法的比较

4.6 实验：logistic 回归、LDA、QDA、KNN

（1）股票市场数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86

"   首先对 ISLR 库中的 Smarket 数据集进行统计分析。数据集包含 2001~2005 共 1250 
天里标普500指数的投资回报率。具体变量：
    Lag1 ~ Lag5：过去的 5 个交易日的投资回报率
    Volume：当天成交量
    Today：当天的投资回报率
    Direction：走势，Up 或 Down
"
library(ISLR)
dim(Smarket)
names(Smarket)
summary(Smarket)
pairs(Smarket)
attach(Smarket)

"------------------------ Logistic Regression ------------------------"

# 将数据分为训练集和测试集
train <- Smarket[(Year<2005), ]
test <- Smarket[!(Year<2005), ]

# 使用广义线性模型，其中包含了 logistic 模型
glm_mod <- glm(Direction~Lag1+Lag2+Lag3+Lag4+Lag5+Volume,
              data = train,
              family = binomial)
summary(glm_mod)
# 模型的系数
coef(glm_mod)
summary(coef(glm_mod))

# 预测在给定输入情况下，市场上涨的概率
glm_mod_prob <- predict(glm_mod, test, type='response')
# 将概率转化为离散变量 Up 和 Down
glm_mod_pred <- rep('Down', 252)
glm_mod_pred[glm_mod_prob > 0.5] <- 'Up'

# 计算混淆矩阵
table(glm_mod_pred, test$Direction)
=====================================
> table(glm_mod_pred, test$Direction)
glm_mod_pred Down Up
        Down   77 97
        Up     34 44
=====================================

# 计算正确率
mean(glm_mod_pred == test$Direction)	# 0.4801587

# 优化模型：减少变量，选择 p 值较低的变量进行拟合。

"-------------------- Linear Discriminant Analysis --------------------"

library(MASS)

# 模型拟合
lda_mod <- lda(Direction~Lag1+Lag2, data=train)
plot(lda_mod)

# 计算预测值
lda_mod_pred <- predict(lda_mod, test)
names(lda_mod_pred)

# 计算混淆矩阵和正确率
table(lda_mod_pred$class, test$Direction)
mean(lda_mod_pred$class == test$Direction)

"------------------ Quadratic Discriminant Analysis ------------------"

qda_mod <- qda(Direction~Lag1+Lag2, data=train)
qda_mod_pred <- predict(qda_mod, test)
table(qda_mod_pred$class, test$Direction)
mean(qda_mod_pred$class == test$Direction)

"------------------------- K Nearest Neighbor -------------------------"

library(class)

# 准备数据
train.X <- cbind(Lag1, Lag2)[(Year<2005), ]
train.Y <- Direction[(Year<2005)]
test.X <- cbind(Lag1, Lag2)[!(Year<2005), ]

# 因为 KNN 算法具有随机性，需要 set.seed
set.seed(1)
knn.pred <- knn(train.X, test.X, train.Y, k=1)	# 更改 k 值寻找最佳拟合
table(knn.pred, test$Direction)
mean(knn.pred == test$Direction)

（2）Caravan 保险数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

attach(Caravan)

"   由于KNN分类模型的原理是通过圈定距离最近的观测来实现
    于是变量的尺度将对结果产生影响
    取值范围较大的变量比较小的变量对距离有更大的影响
    假设数据集包含 salary 和 age
    那么以美元和年来衡量的时候，与以日元和分钟来衡量的时候，会产生完全不同的分类结果
    解决办法：对数据进行标准化，使变量以0为均值，以1为标准差
"
# 标准化数据
standardized.X <- scale(Caravan[, -86])
var(standardized.X[, 1])
# 分成训练集和测试集
train.X <- standardized.X[-(1:1000), ]
test.X <- standardized.X[(1:1000), ]
train.Y <- Purchase[-(1:1000)]
test.Y <- Purchase[(1:1000)]

# KNN 模型
knn.pred <- knn(train.X, test.X, train.Y, k=5)
table(knn.pred, test.Y)
# 错误率
mean(test.Y != knn.pred)
mean(test.Y != 'No')

# logistic 模型
glm.fit <- glm(Purchase~., data=Caravan, family=binomial, subset=-(1:1000))
glm.probs <- predict(glm.fit, Caravan[(1:1000), ], type='response')
glm.pred <- rep('No', 1000)
glm.pred[glm.probs>0.5] <- 'Yes'
table(glm.pred, test.Y)
# 调整 logistic 模型预测的阈值
glm.pred<-rep('No',1000)
glm.pred[glm.probs>0.25]<-'Yes'
table(glm.pred,test.Y)
目录
    文章标签
    R 数据分析 Python RCM 笔记 总结 编程语言 数据可视化 统计分析 商业分析 机器学习 爬虫 转载 市场分析 MySQL 数据库 神经网络 计算机视觉 Java