Python 解决方案:https://github.com/hardikkamboj/An-Introduction-to-Statistical-Learning
第五章 重抽样方法
- 通过反复从训练集中抽取样本,然后对每一个样本拟合一个感兴趣的模型,来获得关于拟合模型的附加信息。
- 重抽样方法可能产生计算量上的代价,因为需要反复地进行拟合
- 两种最常用的重抽样方法:
- 交叉验证法(cross-validation)
- 自助法(bootstrap)
- 交叉验证法可用来估计一种特定的统计学习方法的测试误差,来评价该方法的表现,或为该方法选择合适的光滑度。将上述过程分别称为模型评价和模型选择。
- 自助法应用范围很广,最常用于为一个参数估计或一个统计学习方法提供关于准确度的测量。
5.1 交叉验证法
上一章讲到训练错误率和测试错误率之间存在较大的区别,这是验证训练模型时存在的主要问题。但是实际中经常缺少作为测试集的数据,对此有很多方法根据可获得的训练数据估计测试错误率,一些方法也使用数学方法对训练错误率进行修正。在本节中主要考虑保留训练数据的一个子集进行测试
- 5.1.1 验证集方法(validation set approach)
- 原理:将观测集随机地分为两部分,一个训练集(training set)和一个验证集(validation set),或称为保留集(hold-out set)。
- 缺陷:测试错误率波动较大(由于随机分割);用于训练的观测数据量减少。
- 5.1.2 留一交叉验证法(leave-one-out cross-validation)
- 原理:保留一个观测作为验证数据,其他作为训练数据。重复上述过程 n 次得到 n 个均方误差 MSE
- 相对于验证集方法,LOOCV 方法的优缺点:
- 优点:不容易高估测试错误率;减小了波动性。
- 缺点:由于需要进行多次的拟合,计算量很大。
- 5.1.3 k 折交叉验证法(k-fold CV)
- 原理:LOOCV 的一种替代,由重复拟合 n 次改为重复拟合 k 次
- 5.1.4 k 折交叉验证法的“偏差-方差”权衡
- LOOCV 方法会产生一个近乎无偏的估计,但是方差较大。而选择适当的 k 值,k 折交叉验证法的方差会小很多。一般选取 k=5 或 k=10。
- 5.1.5 交叉验证法在分类问题上的应用
- 在定量数据的交叉验证中,取 MSE 的均值;
- 而对于定性问题,取错误率 Err 的均值。
5.2 自助法(bootstrap)
- 自助法是一种统计工具,用于衡量一个指定的统计量或统计学习中的不确定因素,如一个线性模型系数的标准差。
5.3 实验:交叉验证与自助法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
library(ISLR)
set.seed(1)
attach(Auto)
"------------------------------ 验证集方法 ------------------------------"
# 估计在 Auto 数据集上拟合多个线性模型产生的测试错误率
train <- sample(392, 196)
lm.fit <- lm(mpg~horsepower, data=Auto, subset=train)
# 均方差 MSE
mean((mpg-predict(lm.fit, Auto))[-train]^2) # 22.28447
# 多项式模型
lm.fit2 <- lm(mpg~poly(horsepower, 2), data = Auto, subset = train)
lm.fit3 <- lm(mpg~poly(horsepower, 3), data = Auto, subset = train)
mean((mpg-predict(lm.fit2,Auto))[-train]^2) # 16.4932
mean((mpg-predict(lm.fit3,Auto))[-train]^2) # 16.4776
"---------------------------- 留一交叉验证法 ----------------------------"
library(boot)
# 使用 boot::cv.glm 对 glm 模型进行交叉验证
glm.fit <- glm(mpg~horsepower, data=Auto)
cv.err <- cv.glm(Auto, glm.fit)
# 交叉验证结果
cv.err$delta
"---------------------------- k 折交叉验证法 ----------------------------"
set.seed(17)
cv.error.10 <- rep(0, 10)
for (i in 1:10){
glm.fit <- glm(mpg~poly(horsepower, i), data=Auto)
cv.error.10[i] <- cv.glm(Auto, glm.fit, K=10)$delta[1]
}
plot(cv.error.10)
"------------------------------- 自助法 -------------------------------"
# 自助法几乎可以应用在所有情形,而不要求复杂的数学运算。
# 先创建一个计算统计量的函数,然后使用 boot 函数反复从数据集中有放回地抽取观测执行
# 创建一个计算感兴趣的统计量的函数
alpha.fn <- function(data, index){
X <- data$X[index]
Y <- data$Y[index]
output <- (var(Y)-cov(X,Y)) / (var(X)+var(Y)-2*cov(X,Y))
return (output)
}
# 计算统计量
alpha.fn(Portfolio, 1:100)
# 随机观测序列的统计量
alpha.fn(Portfolio, sample(100, 100, replace=TRUE))
# 自主法多次计算
boot(Portfolio, alpha.fn, R=100)
=====================================================
> boot(Portfolio, alpha.fn, R=100)
ORDINARY NONPARAMETRIC BOOTSTRAP
Call:
boot(data = Portfolio, statistic = alpha.fn, R = 100)
Bootstrap Statistics :
original bias std. error
t1* 0.5758321 0.00278335 0.08577495
=====================================================
第六章 线性模型选择与正则化
- 标准的拟合线性模型的方法为最小二乘法,本章讨论其替代方法以及优化。
- 优化的目标是更高的预测准确率和更好地模型解释力
- 预测准确率:
- 当相应变量与预测变量有近似线性关系,OLS 估计的偏差较小;
- 当观测数量 n 远远大于参数个数 p,OLS 估计的方差通常较低;
- 当 p>n,OLS 估计不唯一。
- 模型解释力:当模型存在非线性或者与模型无关的变量,OLS 通过系数为 0 提高解释力;本章将介绍几种自动进行特征选择和变量选择的方法。
- 主要的替代方法:子集选择、压缩估计、降维法
6.1 子集选择
- 6.1.1 最优子集选择
- 原理:
- 对 p 个预测变量的所有可能组合分别使用最小二乘法回归进行拟合
- 对含有1个预测变量的模型,拟合 p 个模型;
- 对含有两个预测变量的模型,拟合 p(p-1)/2 个模型
- 以此类推。最后选择一个最优的模型。
- 原理:
- 6.1.2 逐步选择
- 6.1.3 选择最优模型
6.2 压缩估计方法
上节的子集选择方法使用最小二乘法对包含预测变量子集的线性模型进行拟合。除此之外,还可以使用对系数进行约束或加惩罚的技巧。也就是将系数向 0 的方向压缩,以此提升拟合效果。常用的两种约束方法是 岭回归 和 lasso。
- 6.2.1 岭回归(ridge regression)
- 原理:第三章介绍了最小二乘法,通过最小化 RSS 进行拟合。而岭回归通过最小化
RSS + lambda*sum(beta^2)拟合。lambda >= 0是调节参数,需单独确定。增加的项称为惩罚项,lambda 越大,压缩效果越明显,系数估计结果越趋于 0。 - 注意到压缩的系数不应该包括 beta0,因为我们的目的是家所有缩减预测变量的系数,而不是缩减截距。因为截距用于测量当预测变量全为 0 时响应的均值。
- l2范数:beta 系数平方求和再开方,衡量 beta 向量到原点的距离。在岭回归中,当lambda 变大,l2 范数变小。
- 岭回归优点:
- 与 OLS 相比,RR 衡量了误差和方差。
- 随着 lambda 变大,RR 拟合的光滑度下降,方差降低,同时偏差变大。
- 当最小二乘的方差较大时,RR 拟合可以有效降低方差。同时在计算量上也有微小优势。
- 原理:第三章介绍了最小二乘法,通过最小化 RSS 进行拟合。而岭回归通过最小化
- 6.2.2 lasso
- 岭回归的劣势在于,子集选择方法会选择变量的一个子集进行建模,而 RR 的最终模型包含全部的 p 个变量。增加 lambda 只会减小系数绝对值,而不会剔除任何一个系数。当p的个数较大,不利于模型的解释。
- lasso 原理:在 OLS 的 RSS 函数基础上改为:
RSS + lambda*sum(abs(beta)) - l1范数:beta 绝对值求和
- 与岭回归类似,但是当 lambda 足够大,lasso 使用的 l1 惩罚项可以将某些系数强制设定为0。最后 lasso 回归只保留变量的一个子集,得到“稀疏模型”。原因是 l1 和 l2 范数的约束条件不同,在拟合中添加约束时,l1 范数对应的约束空间为菱形,l2为圆形。(详见教材)
- 进一步对比:RR 和 lasso 并没有哪个是绝对好的。一般情况下,当一部分预测变量是真实有效的,而其他系数非常小的时候,lasso 比较出色。当这些系数都大致相等时,RR 比较出色(然而这都是不能预先知道的)。
- 6.2.3 选择调节参数
- 需要调节的参数为:优化方程中的 lambda 和约束条件中的 s。一般使用交叉验证法选择最优参数。
6.3 降维方法
上述方法的预测变量都来自原始的预测变量集,而降维法将预测变量进行转换,用转换后的变量拟合最小二乘模型。降维方法可以理解为寻找预测变量之间的相关性,主要方法有主成分分析和偏最小二乘。
- 6.3.1 主成分分析(principal components analysis, PCA)
- 第十章将 PCA 作为无监督学习的一种工具进行更详细的讨论,这里将它作为回归降维方法进行介绍。
- 在第一主成分上,数据的变化最大,定义了与数据最接近的那条线,使所有点到该线的垂直距离平方和最小。
- 第二主成分 Z2 是所有与 Z1 无关的原始变量的线性组合中方差最大的。
- 主成分回归方法(PCR):是指构造前 M 个主成分 Z1~ZM,然后以这些主成分作为预测变量进行最小二乘拟合。
- 特性上 PCR 和 lasso 十分类似,甚至可以认为 lasso 是连续型的 PCR。
- 在 PCR 中,M 的值一般通过交叉验证来确定。
- 进行 PCA 时,一般需要对变量进行标准化,使其度量在相同尺度上。否则方差较大的变量将在主成分中占主导地位。
- 6.3.2 偏最小二乘法(partial least squares, PLS)
- 与 PCR 类似,作为降维的手段,取原始变量的线性组合作为新的变量集,然后进行最小二乘线性拟合。
- 与 PCR 不同,PLS 通过有监督的方法进行新的特征的提取,也就是利用了相应变量的信息筛选新变量。这样不仅很好地近似了原始变量,同时与响应变量相关。简单来说,PLS 试图寻找一个可以同时解释预测变量和响应变量的方向。
6.4 高维问题
- 6.4.1 高维数据
- 传统统计学方法有低维数据发展而来,但是现代的数据往往更复杂;特征数目
- 比观测数目大的数据(p>n)称作高维数据。像 OLS 等传统方法已经不适于高维数据。
- 6.4.2 高维度下的问题
- 包括“方差-偏差”权衡问题,过拟合问题等。
- 6.4.3 高维数据的回归
- 前面提到的逐步选择、岭回归、lasso 以及 PCA 可以避免过拟合,可用于高维。
- 维数灾难:特征数过大,引入了无关的特征,影响模型结果。
- 6.4.4 高维数据分析结果的解释
6.5 实验1:子集选择方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
library(ISLR)
fix(Hitters)
names(Hitters)
dim(Hitters)
sum(is.na(Hitters$Salary)) # 存在缺失值
hitters <- na.omit(Hitters) # 移除缺失值
"使用若干个与棒球运动员上一年比赛成绩相关的变量预测运动员的薪水"
# 使用 regsubset() 函数筛选最优模型,用法类似于 lm 函数
library(leaps)
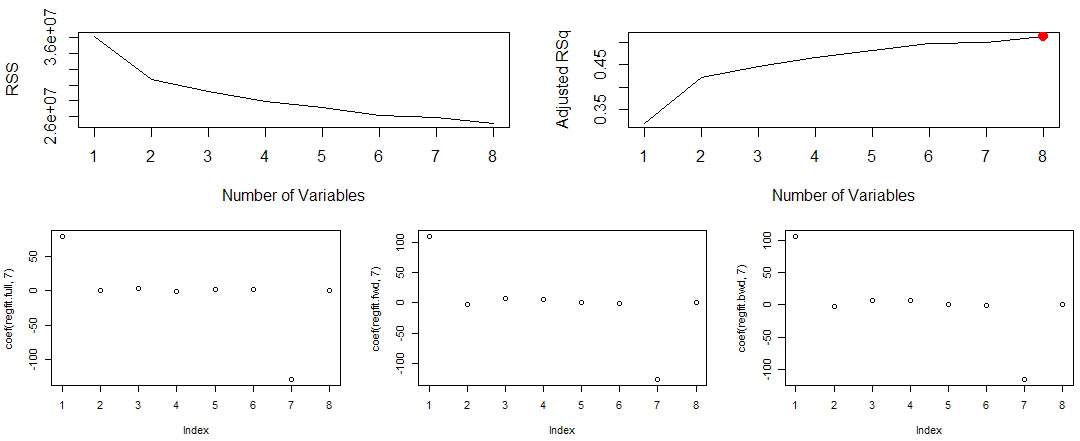
regfit.full <- regsubsets(Salary~., hitters)
summary(regfit.full)$rsq
# 可视化模型结果
par(mfrow=c(1,2))
plot(summary(regfit.full)$rss,
xlab='Number of Variables', ylab='RSS', type='l')
plot(summary(regfit.full)$adjr2,
xlab='Number of Variables', ylab='Adjusted RSq', type='l')
# 标记调整后的R方最大值
M <- which.max(summary(regfit.full)$adjr2)
points(M, summary(regfit.full)$adjr2[M], col='red', cex=2, pch=20)
"向前和向后逐步选择:在上例的基础上添加 method 参数决定 forward 还是 backward"
regfit.fwd <- regsubsets(Salary~., data=hitters, nvmax=19, method='forward')
regfit.bwd <- regsubsets(Salary~., data=hitters, nvmax=19, method='backward')
par(mfrow=c(1,3))
plot(coef(regfit.full, 7))
plot(coef(regfit.fwd, 7))
plot(coef(regfit.bwd, 7))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
"使用验证集方法和交叉验证法选择模型"
set.seed(1)
train <- sample(c(TRUE, FALSE), nrow(hitters), replace=TRUE)
# 在训练集上进行最优子集选择
regfit.best <- regsubsets(Salary~., data=hitters[train, ], nvmax=19)
# 模型预测
test.mat <- model.matrix(Salary~., data=hitters[!train, ])
# 计算预测值和测试值的 MSE
val.errors <- rep(NA, 19)
for (i in 1:19){
coefi <- coef(regfit.best, id=1)
pred <- test.mat[, names(coefi)] %*% coefi
val.errors[i] <- mean((hitters$Salary[!train])^2)
}
which.min(val.errors)
coef(regfit.best, 1)
6.6 实验2:lasso与岭回归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
library(ISLR)
Hitters <- na.omit(Hitters)
# 使用 glmnet::glmnet 函数,需要输入一个自变量矩阵和一个响应变量向量
x <- model.matrix(Salary~., Hitters)[, -1]
# model.matrix 函数不仅可以自动生成与预测变量相对应的矩阵
# 还能自动将定性变量转换为哑变量;注意到glmnet函数只能处理数值型输入
y <- Hitters$Salary
"------------------------------- 岭回归 -------------------------------"
library(glmnet)
grid <- 10^seq(10, -2, length=100)
# glmnet 的 alpha 参数确定模型,0 为岭回归,1 为 lasso
ridge.mod <- glmnet(x, y, alpha=0, lambda=grid)
# glmnet 函数默认将所有变量标准化,可以自定义 standardize=FALSE
dim(coef(ridge.mod))
# 使用l2范数,当 lambda 等于 11498 时的估计结果:
ridge.mod$lambda[50]
coef(ridge.mod)[, 50]
sqrt(sum(coef(ridge.mod)[-1, 50]^2))
# 使用 predict 函数获取新的 lambda 值对应的岭回归系数,如 lambda=50
predict(ridge.mod, s=50, type = 'coefficients')[1:20, ]
# 将数据分成训练集和测试集
set.seed(1)
train <- sample(1:nrow(x), nrow(x)/2)
y_test <- y[(-train)]
# 基于训练集建立岭回归模型,并计算 lambda=4 时测试集的 MSE
ridge.mod <- glmnet(x[train, ], y[train],
alpha=0, lambda=grid, thresh=1e-12)
ridge.pred <- predict(ridge.mod, s=4, newx=x[(-train), ])
MSE <- mean((ridge.pred-y_test)^2) # 101036.8
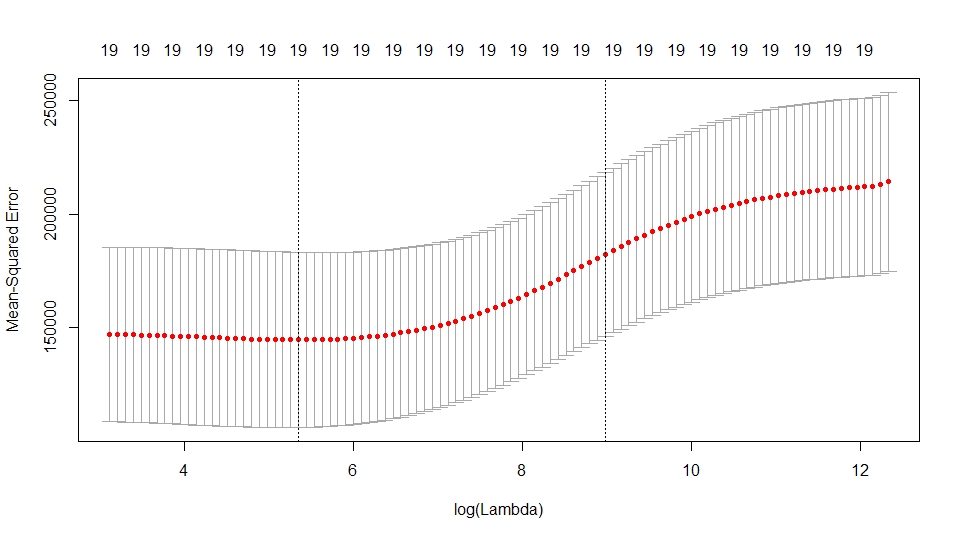
# 使用交叉验证选择参数 lambda
set.seed(1)
cv.out <- cv.glmnet(x[train, ], y[train], alpha=0)
plot(cv.out)
best.lambda <- cv.out$lambda.min
best.lambda # 211.7416
# 使用最佳 lambda 时岭回归的 MSE
ridge.pred <- predict(ridge.mod, s=best.lambda, newx=x[(-train), ])
MSE <- mean((ridge.pred-y_test)^2) # 96015.51
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
"------------------------------- lasso -------------------------------"
# 使用同一个函数同一个数据集,操作与 ridge 类似
lasso.mod <- glmnet(x[train, ], y[train], alpha=1)
plot(lasso.mod)
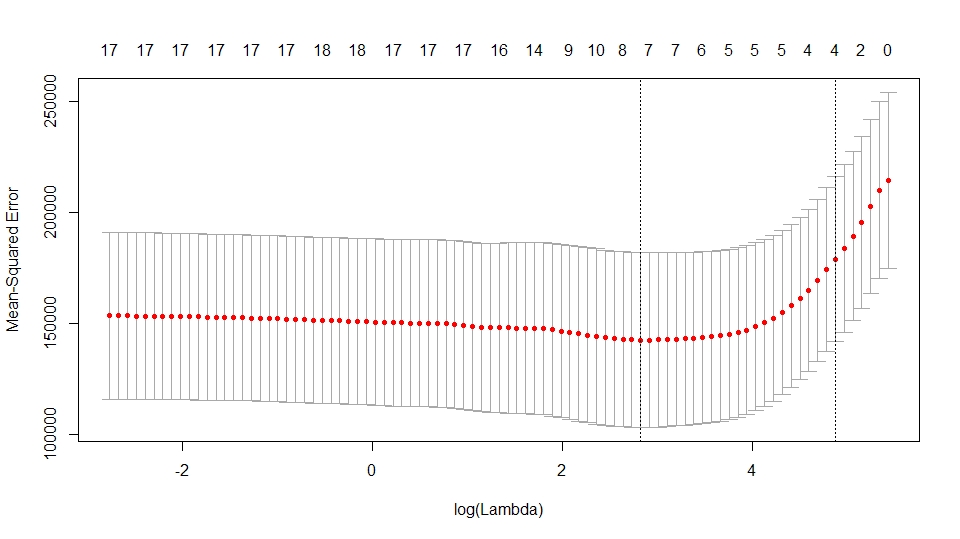
# 使用交叉验证寻找最优参数
set.seed(1)
cv.out <- cv.glmnet(x[train, ], y[train], alpha=1)
plot(cv.out)
best.lambda <- cv.out$lambda.min
# 计算最优参数对应的MSE
lasso.pred <- predict(lasso.mod, s=best.lambda, newx=x[(-train), ])
MSE <- mean((lasso.pred-y_test)^2) # 结果MSE明显小于空模型和最小二乘模型
# lasso的稀疏性:结果模型中只含有7个变量,其他的系数为0
out <- glmnet(x, y, alpha=1, lambda=grid)
lasso.coef <- predict(out, type='coefficients', s=best.lambda)[1:20]
sum(lasso.coef == 0)
6.7 实验3: PCR 与 PLS 回归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
library(ISLR)
Hitters <- na.omit(Hitters)
"------------------- principle component regression -------------------"
# 使用 pls 库中的 pcr 函数实现主成分回归
library(pls)
set.seed(2)
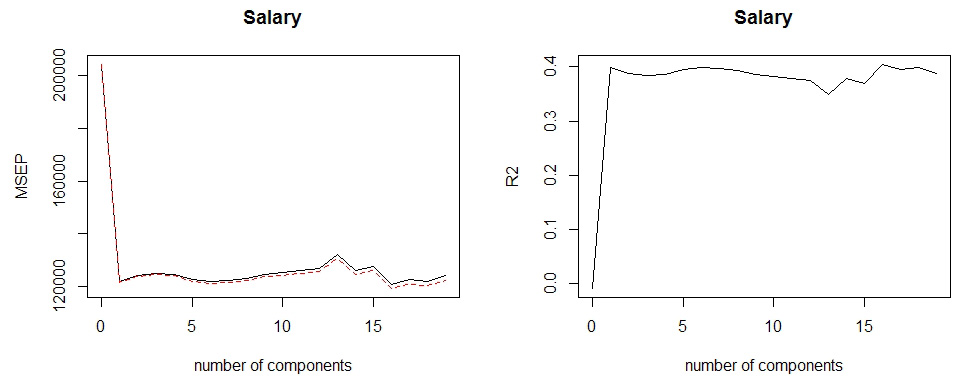
pcr.fit <- pcr(Salary~., data=Hitters, scale=TRUE, validation='CV')
summary(pcr.fit)
# 交叉验证得分(如MSE)图像:
validationplot(pcr.fit, val.type = 'MSEP')
validationplot(pcr.fit, val.type = 'R2')
# 结果当 M=16 时交叉验证误差最小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 下面使用最优子集选择方法
x <- model.matrix(Salary~., Hitters)[, -1]
y <- Hitters$Salary
set.seed(1)
train <- sample(1:nrow(x), nrow(x)/2)
test <- (-train)
y.test <- y[test]
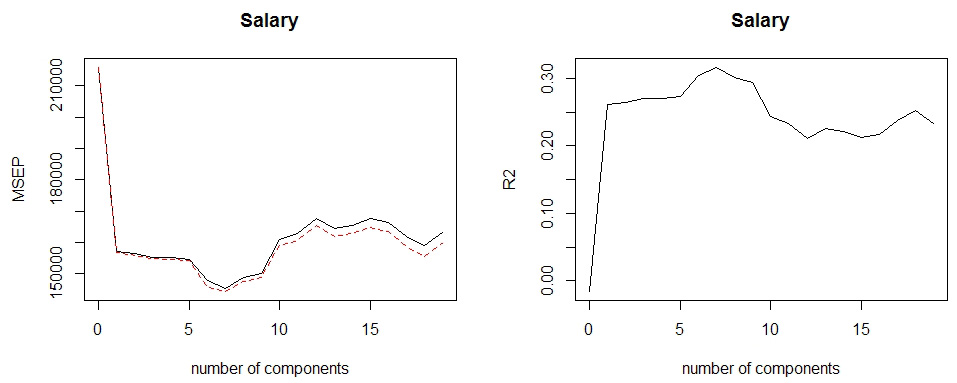
pcr.fit <- pcr(
Salary~.,
data=Hitters, subset=train, scale=TRUE, validation='CV')
validationplot(pcr.fit, val.type='MSEP')
validationplot(pcr.fit, val.type='R2')
# 结果 M=7 时交叉验证误差较小
# 下面计算测试集误差
pcr.pred <- predict(pcr.fit, x[test, ], ncomp=7)
mean((pcr.pred-y.test)^2)
# 拟合结果较 RR 或 lasso 更好,但是由于 PCR 的建模机制,最终模型会更难解释
# 在最优参数上拟合PCR模型
pcr.fit <- pcr(y~x, scale=TRUE, ncomp=7)
=================================================================
> summary(pcr.fit)
Data: X dimension: 263 19
Y dimension: 263 1
Fit method: svdpc
Number of components considered: 7
TRAINING: % variance explained
1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
X 38.31 60.16 70.84 79.03 84.29 88.63 92.26
y 40.63 41.58 42.17 43.22 44.90 46.48 46.69
=================================================================
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
"----------------------- Partial Least Squares -----------------------"
set.seed(1)
# 使用 plsr 函数,用法和 pcr 类似
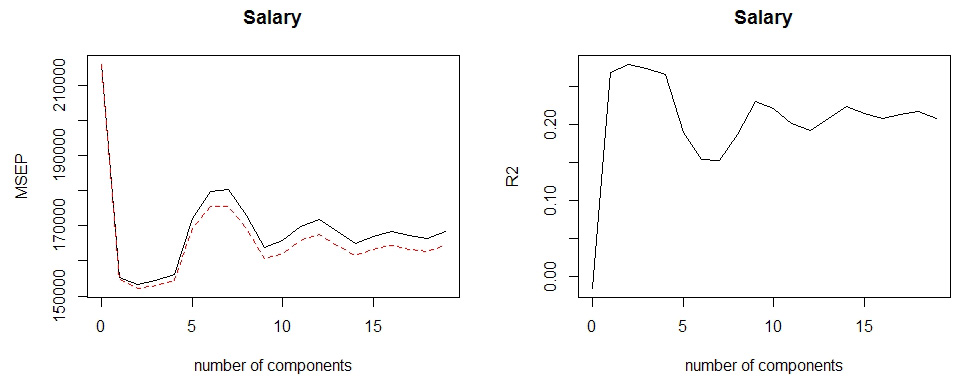
pls.fit <- plsr(
Salary~.,
data=Hitters, subset=train, scale=TRUE, validation='CV')
summary(pls.fit)
validationplot(pls.fit, val.type = 'MSEP')
validationplot(pls.fit, val.type = 'R2')
# 在最佳参数 M=2 上计算测试集 MSE
pls.pred <- predict(pls.fit, x[test, ], ncomp=2)
mean((pls.pred-y.test)^2)
# 最后使用 M=2 在整个数据集上建立 PLS 模型
pls.fit <- plsr(Salary~., data=Hitters, scale=TRUE, ncomp=2)
==================================
> summary(pls.fit)
Data: X dimension: 263 19
Y dimension: 263 1
Fit method: kernelpls
Number of components considered: 2
TRAINING: % variance explained
1 comps 2 comps
X 38.08 51.03
Salary 43.05 46.40
==================================
第七章 非线性模型
- 线性模型更易于描述,实现简便,解释性能和推断理论较成熟。但是在预测上明显不足。需要在线性模型的基础上进行推广。
- 主要推广有:
- 多线式回归(polynomial regression)
- 阶梯函数(step function)
- 回归样条(regression spline)
- 光滑样条(smoothing spline)
- 局部回归(local regression)
- 广义可加模型(generalized additive model)
7.1 多项式回归
- 最简单的推广,就是将标准的线性模型换成一个多项式函数。
7.2 阶梯函数
- 在多项式回归中,使用特征变量的多项式函数作为预测变量,得到全局非线性的模型
- 如果希望得到局部非线性的模型,可以使用阶梯函数进行拟合。也就是将 X 的取值范围分成一些区间,每个区间拟合一个不同的常数。相当于将一个连续变量转换为一个有序的分类变量。
7.3 基函数
- 多项式和阶梯函数回归模型实际上是特殊的基函数方法。其基本原理就是对变量 X 的函数或函数的变换(b1(X), b2(X), … ,bk(X))进行建模。
- 常用的基函数转换除了上述两种,此外常见的还有小波变换和傅里叶级数等。
7.4 回归样条 – 一类光滑的基函数
- 7.4.1 分段多项式
- 分段多项式回归在 X 的不同取值区间拟合独立的低阶多项式函数,而不是在全局范围拟合高阶多项式函数。基本形式可以写为:
y = beta0 + beta1*xi + beta2*xi^2 + beta3*xi^3 + ei
- 其中不同区域的 beta 系数的取值都不一样,系数变化的临界点称为结点(knot)
- 多项式回归可视为无结点的分段多项式回归
- 分段多项式回归在 X 的不同取值区间拟合独立的低阶多项式函数,而不是在全局范围拟合高阶多项式函数。基本形式可以写为:
- 7.4.2 约束条件与样条
- 对于一个只有一个结点的三次多项式,共使用了 8 个自由度。
- 为了使拟合曲线不过于光滑,并且结点之间没有跳跃,需要增加约束条件(即:连续性、一阶导数连续性、二阶导数连续性)。增加的每个约束都会有效地释放一个自由度,降低模型的复杂度。
- 在一般情况下,与 K 个结点一同使用的三次样条会产生 4+K 个自由度。
- 7.4.3 样条基函数
- 7.4.4 确定结点的个数和位置
- 7.4.5 与多项式回归对比
7.5 光滑样条
- 7.5.1 光滑样条的简介
- 上一节的回归样条方法:首先设定结点,然后产生一系列基函数,最后使用最小二乘法估计样条函数的系数。本节使用不同的方法。
- 7.5.2 选择光滑参数 lambda
7.6 局部回归
- 局部回归是拟合光滑非线性函数的另一种方法。在对一个观测 x0 进行拟合时,该方法只使用到这个点附近的观测。
- 变系数模型:局部回归的一种推广,一些变量进行全局回归,另外的进行局部回归。
7.7 广义可加模型
GAM 提供了一种对标准线性模型进行推广的框架。在这个框架中,每一个变量用一个非线性函数进行替换,同时保持模型整体的可加性。
- 7.7.1 用于回归问题的 GAM
- 前面的样条函数、局部回归、多项式回归或者之前章节的一些函数组合都可以用来产生 GAM。
- GAM 的优点和不足:主要局限在于模型的形式被限定为可加形式,在多变量的情况下,通常会忽略掉有意义的交互项
- 7.7.2 用于分类问题的 GAM
- 拟合给定预测变量值时,响应变量的值为 1 的概率,类似 logistic 回归。
7.8 实验:非线性建模
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
library(ISLR)
attach(Wage)
"------------------------ 多项式回归和阶梯函数回归 ------------------------"
# 拟合 wage 的自由度为 4 的多项式模型
fit <- lm(wage~poly(age, 4), data = Wage)
coef(summary(fit))
# 更直接的方法
fit2 <- lm(wage~poly(age, 4, raw=TRUE), data = Wage)
coef(summary(fit2))
# 拟合fit2的等价形式
fit2a <- lm(wage~age+I(age^2)+I(age^3)+I(age^4), data = Wage)
fit2b <- lm(wage~cbind(age, age^2, age^3, age^4), data = Wage)
# 接下来构造一组age的值,进行预测和评估
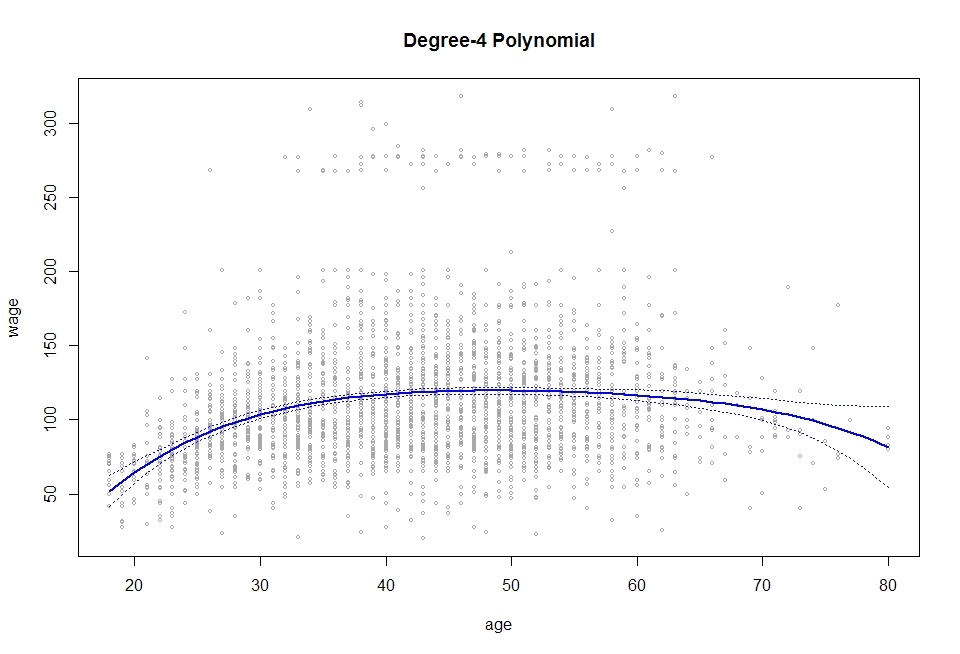
agelims <- range(age)
age.grid <- seq(from=agelims[1], to=agelims[2])
preds <- predict(fit, newdata = list(age=age.grid), se=TRUE)
se.bands <- cbind(preds$fit + 2*preds$se.fit, preds$fit - 2*preds$se.fit)
# 画出数据散点图以及用4次多项式函数拟合的结果
plot(age, wage, xlim = agelims, cex=0.5, col='darkgrey')
title('Degree-4 Polynomial')
lines(age.grid, preds$fit, lwd=2, col='blue')
matlines(age.grid, se.bands, lwd=1, col='blue', lty=3)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
"-------------------------------- 样条 --------------------------------"
# 使用 splines 包中的 bs 函数,默认生成3次样条
library(splines)
fit <- lm(wage~bs(age, knots = c(25, 40, 60)), data=Wage)
# 进行预测与评估
pred <- predict(fit, newdata = list(age=age.grid), se=TRUE)
plot(age, wage, col='gray')
lines(age.grid, pred$fit, lwd=2)
lines(age.grid, pred$fit + 2*pred$se.fit, lty='dashed')
lines(age.grid, pred$fit - 2*pred$se.fit, lty='dashed')
"--------------------- Generalized Additive Model ---------------------"
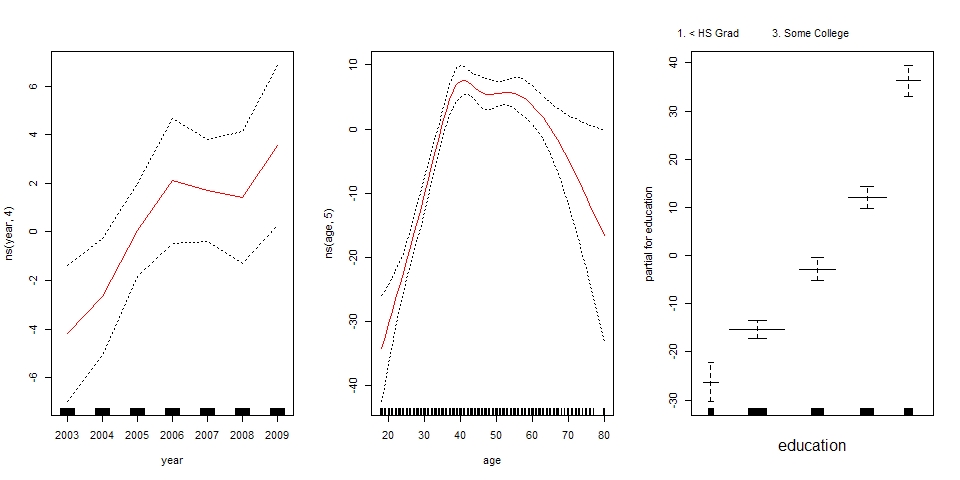
# 使用 education 以及 year 和 age 的自然样条函数作为预测变量拟合 GAM
gam <- lm(wage~ns(year,4)+ns(age,5)+education, data=Wage)
# 接下来使用 gam 包中的 s() 函数拟合光滑样条而不是自然样条
library(gam)
gam.m3 <- gam(wage~s(year,4)+s(age,5)+education, data=Wage)
# 画出结果
par(mfrow=c(1,3))
plot(gam.m3, se=TRUE, col='blue')
# plot 能识别出 gam 对象,实际上是调用 plot.Gam() 函数进行绘图
plot.Gam(gam1, se=TRUE, col='red')