Python 解决方案：https://github.com/hardikkamboj/An-Introduction-to-Statistical-Learning

教材介绍：https://book.douban.com/subject/26430936/

相关资源：http://faculty.marshall.usc.edu/gareth-james/ISL/

第八章基于树的方法

本章介绍基于树的（tree-based）回归和分类方法，这些方法主要根据分层（stratifying）和分割（segmenting）的方式，将预测变量空间划分为一系列简单区域。对某个给定待预测的观测值，用它所属区域中的训练集的平均值或众数进行预测。
由于划分空间的分裂规则可以被概括为一棵树,又称作决策树（decision tree）方法。
基于树方法简便且易于解释，但准确率低于第六章和第七章的指导学习方法。将大量的树进行集成可以极大的提升预测准确性，但是会损失一些解释性。

8.1 决策树的基本原理

8.1.1 回归树（regression tree）
- 最后划分出的区域称作树的终端结点（terminal node）或树叶（leaf）。决策树通常是由上往下画的，树叶位于树的底部。
- 沿着树将预测变量空间分开的点称为内部结点（internal node），各个结点的连接部分称为分支(branch)。
- 通过特征空间分层预测
- 建立回归树的一般过程：
  - 将预测变量空间分割成 J 个不重叠的区域 R1~RJ，然后对落入区域 Rj 的每个观测值进行预测（取该区域上训练集的响应值的算术平均）。
- 递归二叉分裂（recursive binary splitting）：一种自上而下的、贪心的方法。从顶部开始，每个结点分割两个分支。贪心（greedy）指在建立树的每一步中，最优的分裂只取决于当前的一步，而不考虑未来。
- 树的剪枝：
  - 上述方法会有良好的预测结果，但是很可能造成过拟合，原因是这样产生的树可能过于复杂。
  - 裂点更少，区域数更少的树会有更小的方差和更好的解释性（以增加微小的偏差为代价）。一种策略是：仅当分裂使残差平方和的减小量达到某个阈值时，才分裂该结点。其缺点是：过于短视，因为一个结点很可能在以后的分裂中使 RSS 大度地减小。
  - 更好的策略是：形成一颗较复杂的树，再通过剪枝（prune）得到子树（subtree）。但由于子树的数量可能极其庞大，对对每一棵子树都进行交叉验证会太复杂。
  - 解决的方案有：代价复杂性剪枝（cost complexity pruning），也称作最弱联系剪枝（weakest link pruning）
8.1.2 分类树（classification tree）
- 与回归树类似，区别在于分类树用来预测定性变量。构造与回归树也类似,使用了递归二叉树分裂。但是 RSS 指标替换为分类错误率
8.1.3 树与线性模型的比较
- 当存在复杂的高度非线性，基于树方法将更优。
8.1.4 树的优缺点
- 解释性强；更接近人的决策模式；可以用图形直观表示；可以直接处理定性的预测变量而不需要创建哑变量。缺点是预测不够准确。

8.2 装袋法、随机森林和提升法

8.2.1 装袋法（bagging）
- 也称自助法聚集（bootstrap aggregation），类似于第五章的自助法。通过自助抽样创建初始训练集的多个副本，分别建立决策树，最后将这些树结合起来。
- 袋外误差估计
- 变量重要性的度量
8.2.2 随机森林（random forest）
- 通过对树作去相关处理，实现了装袋法的改进。
8.2.3 提升法（boosting）
- 同为装袋法的改进

8.3 实验：决策树

library(ISLR)
library(tree)
library(MASS)
library(randomForest)
library(gbm)

（1）构建分类树 – Carseats 数据集

attach(Carseats)

# 由于 Sales 为连续变量，需要记为二元变量
High <- ifelse(Sales <= 8, 'No', 'Yes')
# 加入原数据集
Carseats <- data.frame(Carseats, High)
# 分集
set.seed(1)
train <- sample(1:nrow(Carseats), 200)
Carseats.test <- Carseats[-train, ]
High.test <- High[-train]

# 使用除了 Sales 外的所有变量拟合 High 变量，tree() 的语法与 lm() 类似
tree.carseats <- tree(High~.-Sales, data=Carseats, subset=train)
tree.pred <- predict(tree.carseats, Carseats.test, type='class')
table(tree.pred, High.test)
plot(tree.carseats)
text(tree.carseats, pretty=0)

# 尝试进行减枝优化模型
set.seed(2)
# 交叉验证确定最优树
cv.caeseats <- cv.tree(tree.carseats, FUN=prune.misclass)
names(cv.carseats)    #分别给出叶子数、错误率、复杂性参数值、剪枝方法
# 画出错误率 dev 对 size 和 k 的函数
par(mfrow=c(1,2))
plot(cv.carseats$size, cv.carseats$dev, type='b')
plot(cv.carseats$k, cv.carseats$dev, type='b')
# 树越大错误率越低，复杂度越高

（2）构建分类树 – Boston 数据集

# 创建训练集并根据训练集生成树
set.seed(3)
train <- sample(1:nrow(Boston), nrow(Boston)/2)
tree.boston <- tree(medv~., Boston, subset=train)
summary(tree.boston)
# 画出树
plot(tree.boston)
text(tree.boston, pretty=0)

# 交叉验证并生成剪枝树
cv.boston <- cv.tree(tree.boston)
plot(cv.boston$size, cv.boston$dev, type='b')
prune.boston <- prune.tree(tree.boston, best=5)
plot(prune.boston)
text(prune.boston, pretty=0)

# 用未剪枝的树对测试集进行预测
yhat <- predict(tree.boston, newdata=Boston[-train, ])
boston.test <- Boston[-train, 'medv']
abline(0, 1)
mean((yhat-boston.test)^2)

（3）装袋法与随机森林

# 装袋法：随机森林的一种特例
set.seed(4)
bag.boston <- randomForest(medv~., data=Boston, subset=train, mtry=13, 
                           importance=TRUE)
# mtry=13 意味着每个结点要考虑全部的 13 个变量。
# 使用测试集进行评估:
yhat.bag <- predict(bag.boston, newdata=Boston[-train, ])
plot(yhat.bag, boston.test)
abline(0, 1)
mean((yhat.bag-boston.test)^2)          # 13.86875

# 使用ntree参数改变生成树的数量
bag.boston <- randomForest(medv~., data=Boston, subset=train, mtry=13,
                           ntree=25)
yhat.bag <- predict(bag.boston, newdata=Boston[-train, ])
mean((yhat.bag-boston.test)^2)          # 14.64803

# 生成随机森林与装袋法一样，只不过 mtry 小于变量数量，默认为 p/3
set.seed(5)
rf.boston <- randomForest(medv~., data=Boston, subset=train, mtry=6,
                          importance=TRUE)
yhat.rf <- predict(rf.boston, newdata=Boston[-train, ])
mean((yhat.rf-boston.test)^2)           # 13.72421
# 使用 importance 函数查看个变量的重要性,并绘图显示
importance(rf.boston)
varImpPlot(rf.boston)

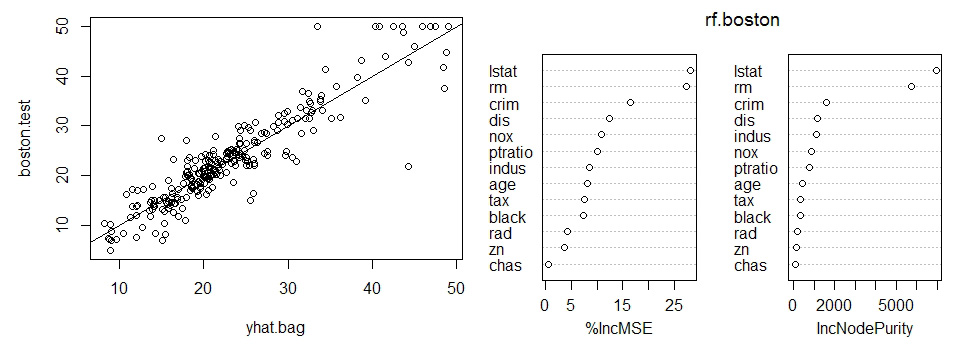
（4）提升法

"   用 gbm 包对 Boston 数据集建立回归树
    由于是回归问题，gbm() 函数的 distribution 参数选用'gaussian'
    如果是二分类问题则选用 'bernoulli'
    对象 n.tree=5000 表示提升法模型共需要 5000 棵树
    选项 interaction.depth=4 限制每棵树的深度。
"
library(gbm)
set.seed(1)
boost.boston <- gbm(medv~., data=Boston[train, ], 
                    distribution='gaussian', 
                    n.trees=5000, 
                    interaction.depth=4)

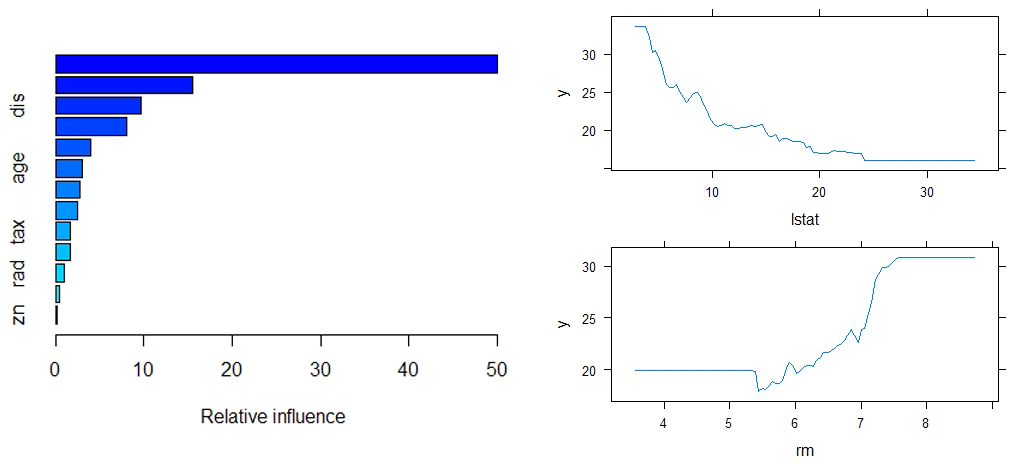
# 使用summary生成相对影响图，并输出相对影响统计数据
summary(boost.boston)
# 画出最重要的两个变量的偏相关图（类似偏导数）
par(mfrow=c(2,1))
plot(boost.boston, i='rm')
plot(boost.boston, i='lstat')

# 使用测试集进行评估
yhat.boost <- predict(boost.boston, newdata=Boston[-train, ], 
                      n.trees=5000)
mean((yhat.boost-boston.test)^2)        # 16.50313
# 结果与随机森林接近

# 使用不用的压缩参数 lambda 进行提升法，默认值是 0.001，现在取 0.2
boost.boston <- gbm(medv~., data=Boston[train, ], 
                    distribution='gaussian', 
                    n.trees=5000, interaction.depth=4, shrinkage=0.2, 
                    verbose=FALSE)
# 测试均方差略低于默认压缩率

第九章支持向量机

支持向量机（support vector machine, SVM）是一种分类方法，在许多问题有较好的效果，是适应性最广的分类器之一。可以看作一类简单直观的最大间隔分类器（maximal margin classifier）。

9.1 最大间隔分类器

9.1.1 超平面（hyperplane）
- 二维空间的超平面是一条直线，三维空间的超平面是一个平面。也就是说，在 p 维空间中，超平面是 p-1 维的平直的子空间。
- 一个 p 维空间的超平面的表达式：
  - beta0 + beta1*X1 + beta2*X2 + ... + beta_p*X_p = 0
- 使上式大于 0 的 X 落在超平面的一侧，使上式小于 0 的 X 落在另一侧
9.1.2 使用分割超平面分类
- 根据训练数据以某种法则找出一个超平面，即一个线性决策边界。进行预测时，测试数据被分到哪一类取决于观测点落到超平面的哪一侧。
9.1.3 最大间隔分类器
- 由于可以找到无数个超平面分割数据，因此需要一个选择标准。一种方法就是最大间隔分类器，也称最优分离超平面（optimal separating hyperplane）
- 具体操作：
  - 首先计算训练集每个观测到一个特定的超平面的垂直距离，这些距离的最小值就是训练观测与分割超平面的距离，称作间隔（margin）
  - 最大间隔超平面就是使间隔最大化的一个分割超平面。
  - 距离分割超平面最近的观测点称作支持向量。
9.1.4 构建最大间隔分类器
9.1.5 线性不可分的情况
- 在许多情况下并不存在分割超平面，因此需要支持向量分类器

9.2 支持向量分类器

9.2.1 概述
- 即使存在分割超平面，上述分类器也经常不可取，因为对观测个体太敏感。
- 支持向量分类器，也称软间隔分类器（soft margin classifier），允许小部分观测被错误分类，而保证分类器的稳定性。
9.2.2 细节
- 落在间隔上或者落在错误的一侧的观测称为支持向量，因为只有这些观测会影响支持向量分类器。
- 支持向量分类器只有一部分观测（支持向量）确定，意味着对于距离超平面较远的观测来说，分类器是鲁棒的。

9.3 狭义的支持向量机 – 由线性决策边界过渡到非线性

9.3.1 使用非线性决策边界分类
- 实际中会遇到非线性的分类。类似回归问题中使用多项式函数的非线性扩展，在支持向量分类器中可以类似地处理非线性问题。
- 例如使用二次多项式或更高阶的多项式扩大特征空间，对于加入二次多项式，原来的 p 个特征将变成 2p 个特征，然后可以在更高维的空间中生成线性的决策边界。
9.3.2 支持向量机
- SVM 是支持向量分类器的一种扩展，使用了核函数（kernel）来扩大特征空间。
- 核函数的使用
9.3.3 心脏数据集的应用

9.4 多分类的SVM

扩展到 K 类主要有两种方法：一类对一类（One versus one），一类对余类。

9.5 与逻辑斯谛回归的关系

9.6 实验：支持向量机

# e1071 包或者 LiblineaR 包都可以实现支持向量分类器和 SVM
library(ISLR)
library(e1071)

（1）支持向量分类器

# 首先生成属于两个类别的观测数据
set.seed(1)
x <- matrix(rnorm(20*2), ncol=2)
y <- c(rep(-1, 10), rep(1, 10))
x[y==1, ] <- x[y==1, ] + 1
# 检查是线性可分，结果非线性可分
plot(x, col=y+3)

# 构建数据集，将响应变量转换成因子变量
data <- data.frame(x=x, y=as.factor(y))
# 拟合支持向量分类器
svm.fit <- svm(y~., data=data, kernel='linear', cost=10, scale=FALSE)
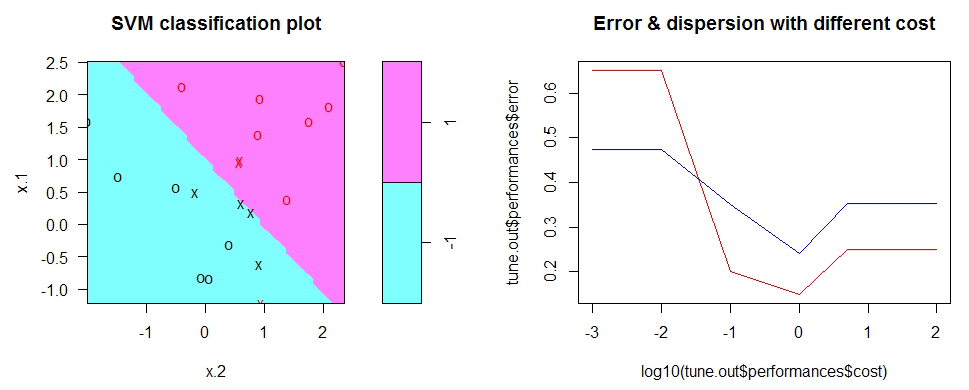
# 可视化分类器
plot(svm.fit, data)
# 查看支持变量
svm.fit$index
# 使用更小的 cost 参数，可以得到更宽的间隔，更多的支持变量

# 使用 tune 函数进行交叉验证调参
set.seed(2)
tune.out <- tune(svm, y~., data=data, kernel='linear',
                ranges = list(cost=c(0.001, 0.01, 0.1, 1, 5, 10, 100))
                )
plot(log10(tune.out$performances$cost), tune.out$performances$error, type='l', col='red')
points(log10(tune.out$performances$cost), tune.out$performances$dispersion, type='l', col='blue')
title(main='Error & dispersion with different cost')

====================================================================
> summary(tune.out$best.model)

Call:
best.tune(method = svm, train.x = y ~ ., data = data, 
          ranges = list(cost = c(0.001, 0.01, 0.1, 1, 5, 10, 100)), 
          kernel = "linear")
Parameters:
   SVM-Type:  C-classification 
 SVM-Kernel:  linear 
       cost:  1 
Number of Support Vectors:  11
 ( 6 5 )
Number of Classes:  2 
Levels:  -1 1
====================================================================

（2）支持向量机

"   使用带核函数的支持向量机：
    kernel='polynomial -- 拟合多项式核函数的 SVM，调节 degree 参数；
    kernel='radial' -- 拟合径向基核函数的 SVM，调节 gamma 参数。
"
set.seed(3)

# 构建具有非线性决策边界的二维特征数据
x <- matrix(rnorm(200*2), ncol=2)
x[1:100, ] <- x[1:100, ] + 2
x[101:150, ] <- x[101:150, ] - 2
y <- c(rep(1, 150), rep(2, 50))
data <- data.frame(x=x, y=as.factor(y))
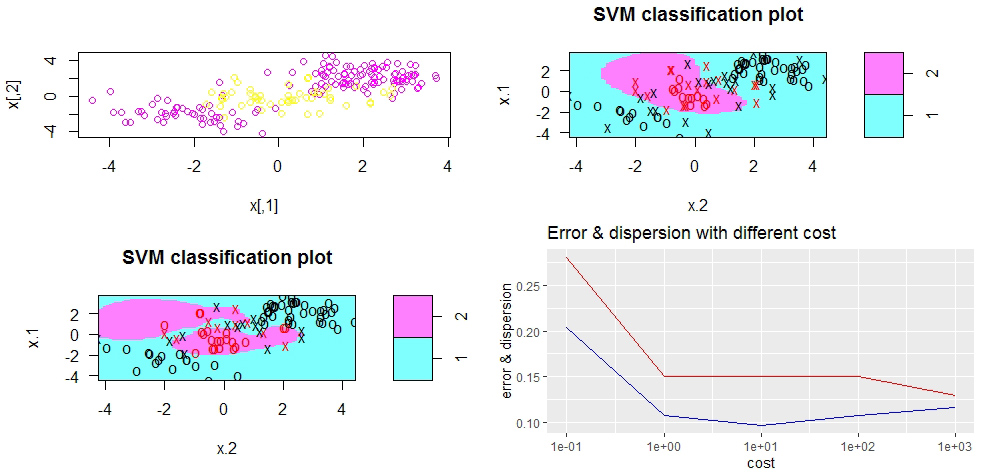
plot(x, col=y+5)

# 分集并拟合，使用径向基核函数，取 gamma=1
train <- sample(200, 100)
svm.fit <- svm(y~., data=data[train, ], kernel='radial', gamma=1, cost=1)
plot(svm.fit, data[train, ])

# 使用更大的 cost 减少误分观测，代价是边界不规则，可能会过拟合
svm.fit <- svm(y~., data=data[train, ], kernel='radial', gamma=1, cost=1e5)
plot(svm.fit, data[train, ])

# 使用 tune 进行交叉验证确定最佳的 gamma 和 cost 值
set.seed(4)
tune.out <- tune(svm, y~., data=data[train, ], kernel='radial',
                ranges=list(cost=c(0.1, 1, 10, 100, 1e3)),
                gamma=c(0.5, 1, 2, 3, 4))
library(tidyverse)
tune.out$performances %>% ggplot(aes(x=cost)) + 
    geom_line(aes(y=error), color='red') + 
    geom_line(aes(y=dispersion), color='blue') + 
    scale_x_log10() + 
    labs(y = 'error & dispersion',
        title = 'Error & dispersion with different cost')

===========================================
> summary(tune.out)
Parameter tuning of ‘svm’:
- sampling method: 10-fold cross validation 
- best parameters:
 cost
 1000
- best performance: 0.13
- Detailed performance results:
   cost error dispersion
1 1e-01  0.28 0.20439613
2 1e+00  0.15 0.10801234
3 1e+01  0.15 0.09718253
4 1e+02  0.15 0.10801234
5 1e+03  0.13 0.11595018
===========================================

# 使用最佳参数在测试集上进行评估
table(tune = dat[-train, 'y'], 
      pred = predict(tune.out$best.model, newx=data[-train, ]))

（3） ROC 曲线（ Receiver Operating Characteristic）

library(ROCR)

# 定义一个函数，在给定的包含每个观测值的 pred 和真实值下，画出ROC曲线
rocplot <- function(pred, truth, ...){
    predob <- prediction(pred, truth)
    perform <- performance(predob, 'tpr', 'fpr')
    plot(perform, ...)
}
# 拟合模型
svmfit.opt <- svm(y~., data=dat[train, ], 
                  kernel='radial', gamma=2, cost=1, decision.values=TRUE)
fitted <- attributes(predict(svmfit.opt, dat[train, ], 
                             decision.values=TRUE))$decision.values
# 绘制ROC曲线
rocplot(fitted, dat[train, 'y'], main='Training Data')

（4）多分类 SVM

"   使用khan数据集，数据集由 2308 个基因的表达测定组成；
    训练集和测试集分别由 63 和 20 个观测组成；"
names(Khan)
dim(Khan$xtrain)
dim(Khan$xtest)
table(Khan$ytrain)
table(Khan$ytest)

# 使用支持向量机预测癌症，由于特征数特别多，使用线性核函数
data <- data.frame(x=Khan$xtrain, y=as.factor(Khan$ytrain))
out <- svm(y~., data=data, kernel='linear', cost=10)
summary(out)
table(out$fitted, data$y)
# 可以看到训练集误差为 0，因为特征空间维度高，产生过拟合

# 测试集误差
data.test <- data.frame(x=Khan$xtest, y=as.factor(Khan$ytest))
pred.test <- predict(out, newdata=data.test)
table(pred.test, data.test$y)

第十章无监督学习（unsupervised learning）

无监督学习是一系列统计工具，研究只有特征数据而没有响应变量的情况。其目标并非预测，而是寻找特征空间的有价值的模式。常见两种无监督学习：主成分分析（PCA）、聚类分析（clustering）。

10.1 无监督学习的挑战

相比于前面介绍的有监督学习，无监督学习更具有挑战性。训练更倾向于主观性，不设定明确的分析目标。评价一个无监督学习的结果非常困难。

10.2 主成分分析

第六章研究主成分回归（PCR）时，解释了主成分方向：特征空间中原始数据高度变异（highly variable）的方向。获取主成分使用了 PCA 方法。

10.2.1 什么是主成分
- 如果要将 p 个特征画出相关矩阵散点图，将有 p(p-1)/2 个散点图。而且每个图只包含数据集很小一部分信息，没有多大价值。使用 PCA 就可以得到一个二维表示来获得数据集的大部分信息。
- 基本思想：n 个观测虽然都在 p 维空间中，但不是所有的维度同样地有价值。PCA 寻找尽可能少的有意义的维度（离散度越高越有价值）。通过PCA找到的每个维度都是原始的 p 个特征的线性组合。
- 第一主成分是变量的标准化线性组合中方差最大的组合：
  - Z1 = phi_11*X_1 + phi_21*X_2 + ... + phi_p1*X_p
  - phi是希腊字母，代表载荷（loading）。标准化（normalized）是指为了防止载荷大小影响方差大小，限定载荷的平方和为 1。寻找第一主成分可以理解为在上述约束下最大化载荷平方和。
10.2.2 主成分的另一种解释
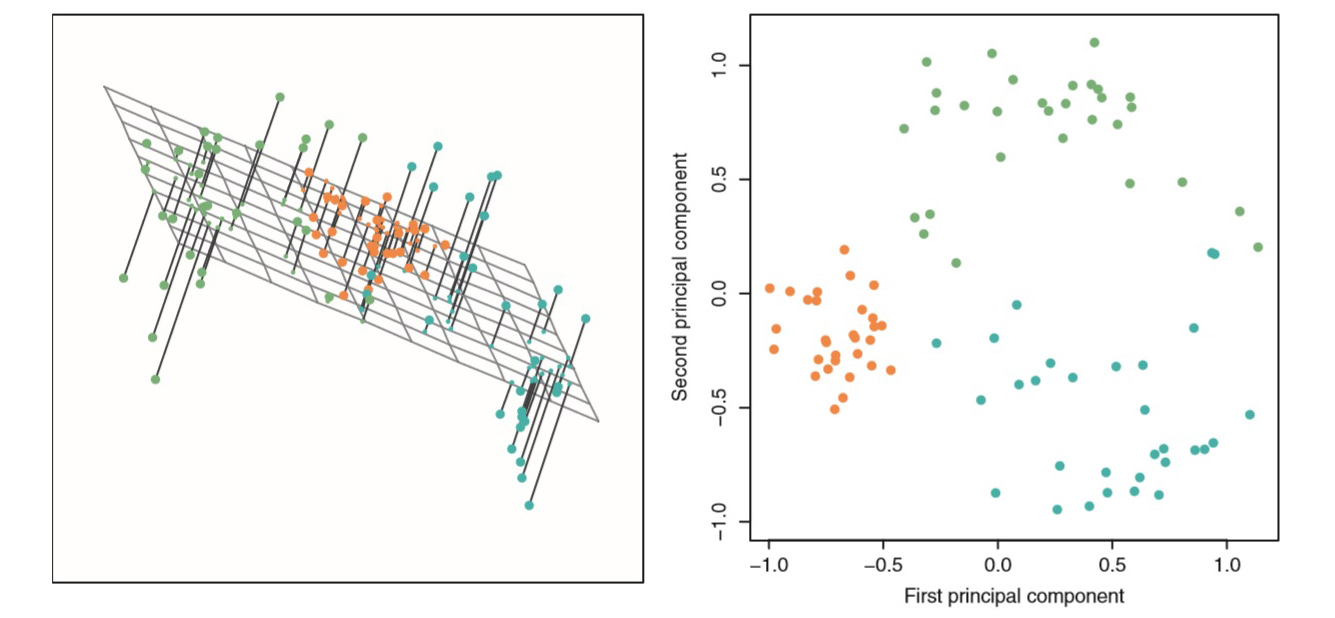
- 上图显示了一个三维数据集的前两个主成分载荷向量。这两个主成分张成一个平面，这个平面在空间中的方向是观测数据方差达到最大的方向。三维数据从主成分载荷方向投影到一个二维平面，得到一张二维图，即主成分得分向量。
- 对此得到主成分分析的另一种解释：主成分提供了一个与观测数据最接近的低维线性空间（我理解为面积最小的投影）。
10.2.3 关于 PCA 的其他方面
- 变量的标准化：在进行 PCA 之前，变量应该中心化使均值为零，还需要进行变量的标准化，某则影响结果。这是 PCA 与其他方法的重要区别。例如线性回归中，变量是否标准化对结果没有影响。
- 主成分的唯一性：除了计算出来的符号正负不同（向量正方向不同），每个主成分的载荷向量是唯一的（即使用不同的软件包计算）。
- 方差的解释比例（proportion of variance explained, PVE）：表示每个主成分解释了多少比例（百分比）的方差。计算公式略。
- 决定主成分的数量：n*p 维的数据矩阵 X 有 min(n-1, p) 个不同的主成分，但是一般不会全部用上。用多少比较好，没有一个最佳答案。
10.2.4 主成分的其他用途

10.3 聚类分析方法

clustering 是在一个数据集中寻找子群或类的方法，应用广泛。基本原则是，是每个类内的观测彼此尽量相似，不同类的差异尽量大。
聚类和 PCA 的目标都是用少量的概括性信息简化数据，但是机制不同：PCA 寻找观测的一个低维表示来解释大部分方差，聚类从观测中寻找同质子类。
主要聚类方法：K 均值聚类（K-means clustering）和系统聚类（hierarchical clustering）；前者预先规定类的数量，后者反之。
10.3.1 K 均值聚类
- K-means 算法：
  - 1.确定 K 值，为每个观测随机初始化 1~K 的数值
  - 2.重复以下直到收敛：
    - a.分别计算 K 个类的中心，即该类中 p 维观测向量的均值向量
    - b.将每个观测分配到距离最近的类中心所属的类（欧氏距离的“最近”）
- 由于 K-means 算法找到的是局部最优解，算法收敛是未必是总体最优解，还跟初始化有关。因此需要进行随机初始化，多次运行再对比找到最优解。
10.3.2 系统聚类法
- 与 K-means 聚类对比，系统聚类法不需要预设类数 K，另外一个优点是可以输出一个好看的有关各观测的树型表示，称作谱系图（dendrogram）
- 一种常见的系统聚类方法：自下而上（bottom-up）的方法，也称凝聚法（agglomerative）。其谱系图由叶子开始聚集到树干，形成一棵倒过来的树。
- 解释谱系图：通过谱系图直观解释系统聚类法，略。
- 算法实现：
  - 1. 计算 n 个观测中所有 n(n-1)/2 对观测数据之间的相异度（如欧氏距离），将每个观测看作一类。
  - 1. 令 i = n, n-1, n-2, … ,2:
      - a.在 i 个类中，比较任意两个类的相异度，找到相异度最小的一对，并结合。用两个类之间的相异度表示两个类在谱系图中交汇的高度
      - b.计算剩余的 i-1 个类中，每两个类的相异度
  - LOOP
- 四种常见的距离形式：最长距离法、最短距离法、类平均法、重心法。
- 相异度指标的选择：一般都是欧氏距离
10.3.3 聚类分析的实践问题
- 小策略撬动大理论：涉及很多方法或指标选择的问题
- 验证聚类结果的问题：得到的是代表数据共性的子类，还是仅仅将噪声聚到了一起？可以通过 p 值进行显著性检验，但是没有公认的好方法。
- 聚类分析的其他考虑：
  - 解释聚类分析结果的一个折中方法：建议对数据集的子集进行聚类分析，这样可以对所得到的类的稳定性有一个整体感知。

10.4 实验

（1）主成分分析

"使用 USArrests 数据集进行 PCA， 数据集包含50个州的观测，4个变量"
library(ISLR)
states <- row.names(USArrests)
variables <- names(USArrests)
# 查看变量的均值和方差，发现相差较大
apply(USArrests, 2, mean)
apply(USArrests, 2, var)

# 因此使用带有标准化的主成分分析
pr.out <- prcomp(USArrests, scale=TRUE)
pr.out$rotation     # 主成分载荷向量
pr.out$x            # 主成分得分向量
pr.out$sdev         # 主成分标准差

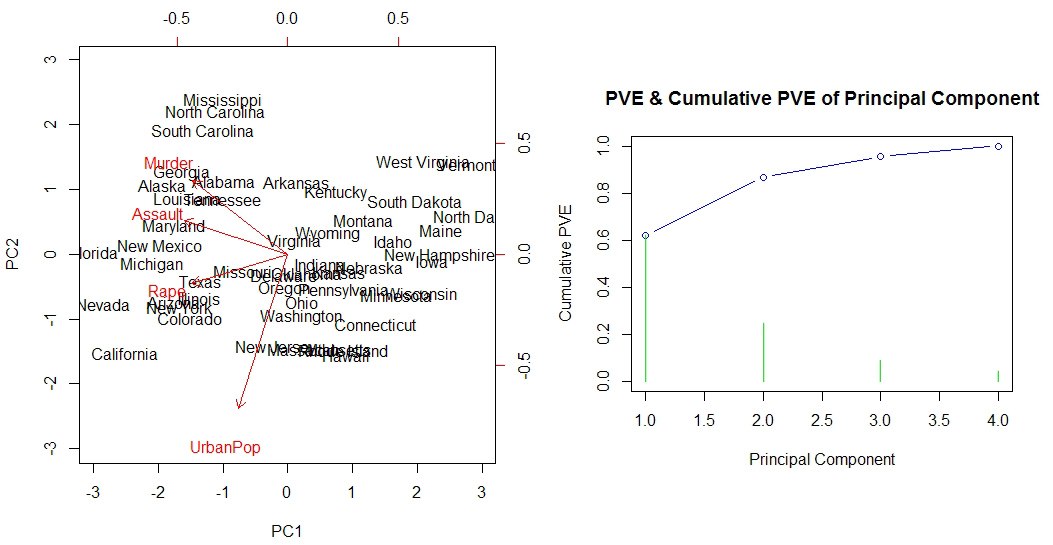
# 绘出前两个主成分的双标图
biplot(pr.out, scale=0)

# 计算每个主成分的方差解释比
pve <- pr.out$sdev^2 / sum(pr.out$sdev^2)
# 绘制每个主成分的 PVE 和累积 PVE
plot(cumsum(pve), 
     xlab='Principal Component', ylab='Cumulative PVE', 
     ylim=c(0,1), type='b', col='blue')
points(pve, ylim=c(0,1), type='h', col='green')
title(main='PVE & Cumulative PVE of Principal Component')

（2）聚类分析

"------------------------------- K Means -------------------------------"

# 创建数据
set.seed(1)
x <- matrix(rnorm(50*2), ncol=2)
x[1:25, 1] <- x[1:25, 1] + 3
x[1:25, 2] <- x[1:25, 2] - 3

# 使用较大的 nstart，可以模拟较多的随机初始化，并选取最佳结果
km.out <- kmeans(x, 2, nstart=20)
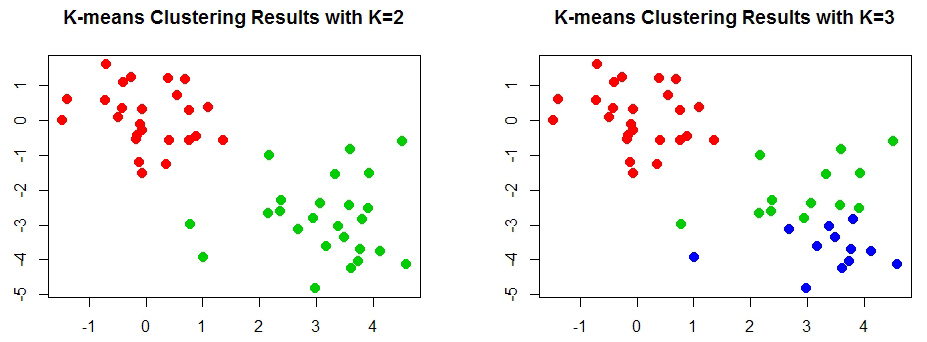
# 可视化模型结果
plot(x, col=(km.out$cluster+1), 
     main='K-means Clustering Results with K=2', 
     xlab='', ylab='', pch=20, cex=2)
# 注意到数据是二维的，容易可视化。对于多位数据，可以绘制前两个主成分的得分向量

# 对数据进行K=3的K均值聚类
set.seed(2)
km.out<-kmeans(x, 3, nstart=20)
plot(x, col=(km.out$cluster+1), 
     main='K-means Clustering Results with K=3', 
     xlab='', ylab='', pch=20, cex=2)

"------------------------------ 系统聚类法 ------------------------------"

# 使用 hclust 函数进行分层聚类，使用不同的距离方式，以欧式距离作为相异度
hc.complete <- hclust(dist(x), method='complete')   # 最长距离法
hc.single <- hclust(dist(x), method='single')       # 最短距离法
hc.average <- hclust(dist(x), method='average')     # 类平均法

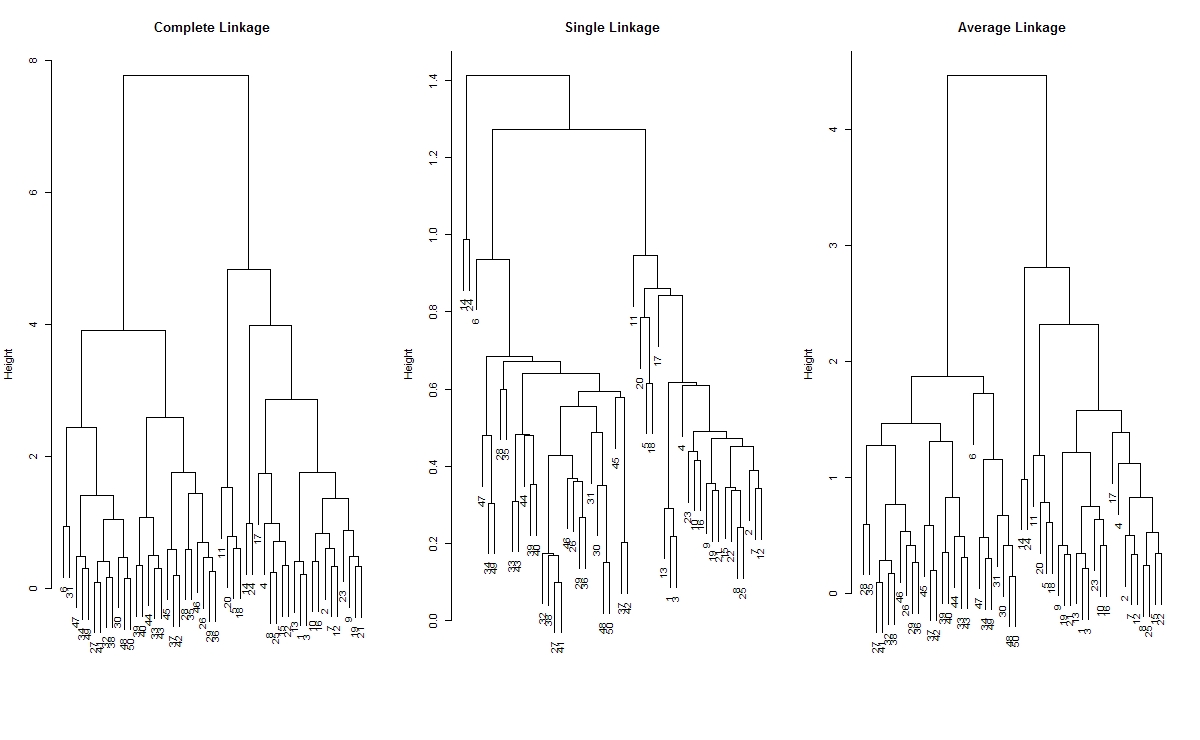
# 绘制谱系图，尽头的每个数字代表一个观测
par(mfrow=c(1,3))
plot(hc.complete, main='Complete Linkage', xlab='', sub='', cex=0.9)
plot(hc.single, main='Single Linkage', xlab='', sub='', cex=0.9)
plot(hc.average, main='Average Linkage', xlab='', sub='', cex=0.9)

# 使用 cutree 函数根据谱系图的切割获取各个观测的类标签
========================================================================
> cutree(hc.complete, 2)
 [1] 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2
[35] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
========================================================================

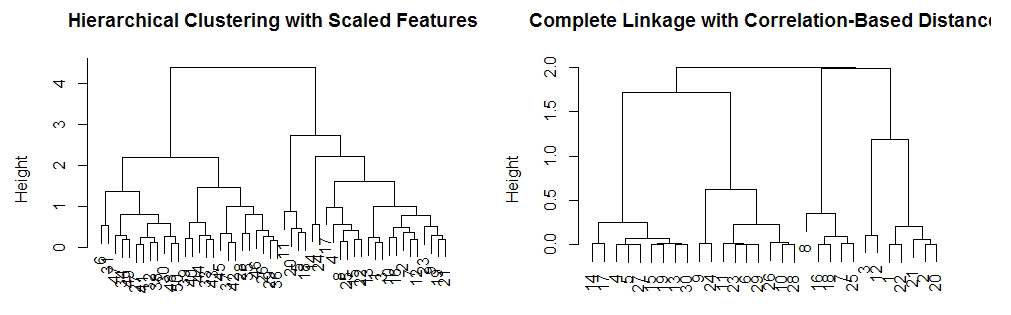
# 对标准化的数据进行系统聚类
x_sc <- scale(x)
plot(hclust(dist(xsc), method='complete'), 
     main='Hierarchical Clustering with Scaled Features',
     xlab='', sub='')

# 修改欧氏距离为基于相关性距离，使用 as.dist() 函数
x <- matrix(rnorm(30*3), ncol=3)
dd <- as.dist(1-cor(t(x)))
plot(hclust(dd, method='complete'), 
     main = 'Complete Linkage with Correlation-Based Distance', 
     xlab='', sub='')

（3）以 NCI60 数据集为例

# PCA 和系统聚类法常用于基因数据的分析
# NCI60 数据集由 64 个细胞的共 6830 个基因表达数据组成

nci.labs <- NCI60$labs      # 癌细胞类型
table(nci.labs)
nci.data <- NCI60$data      # 基因数据
dim(nci.data)

"--------------------- 使用主成分分析查找癌症相关细胞 ---------------------"

# 数据标准化的 PCA
pr.out <- prcomp(nci.data, scale=TRUE)
# 定义函数给每个观测对应的癌症类型分配不同颜色
Cols <- function(vec){
    cols <- rainbow(length(unique(vec)))
    return (cols[as.numeric(as.factor(vec))])
}
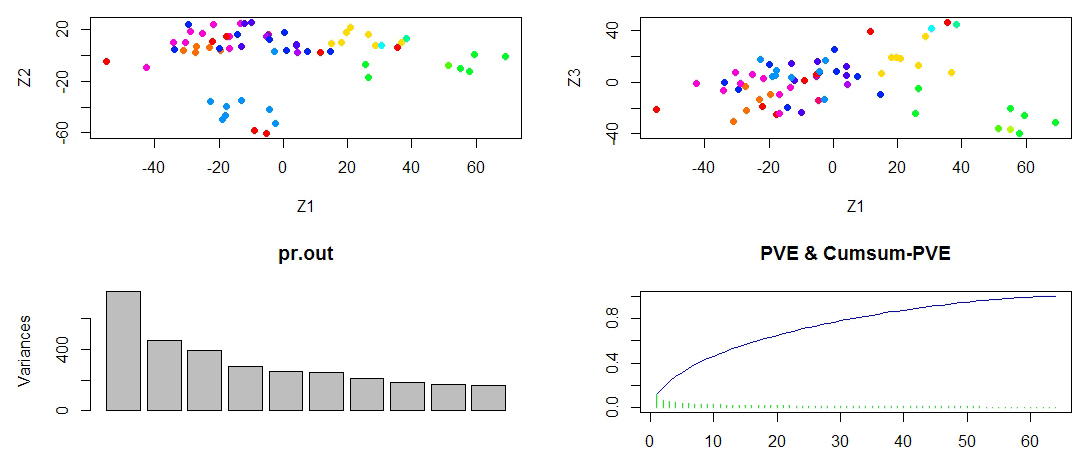
# 对前几个主成分进行可视化，绘制得分向量图
par(mfrow=c(1,2))
plot(pr.out$x[,1:2], col=Cols(nci.labs), pch=19, xlab='Z1', ylab='Z2')
plot(pr.out$x[,c(1,3)], col=Cols(nci.labs), pch=19, xlab='Z1', ylab='Z3')
# 可以看到对于同类癌症的细胞系的前几个主成分得分向量比较接近

# 绘制前几个主成分解释的方差
plot(pr.out)
# PVE 和累计 PVE
pve <- pr.out$sdev^2 / sum(pr.out$sdev^2)
plot(cumsum(pve), xlab='', ylab='', ylim=c(0,1), type='l', col='blue')
points(pve, xlab='', ylab='', ylim=c(0,1), type='h', col='green')
title(main='PVE & Cumsum-PVE')

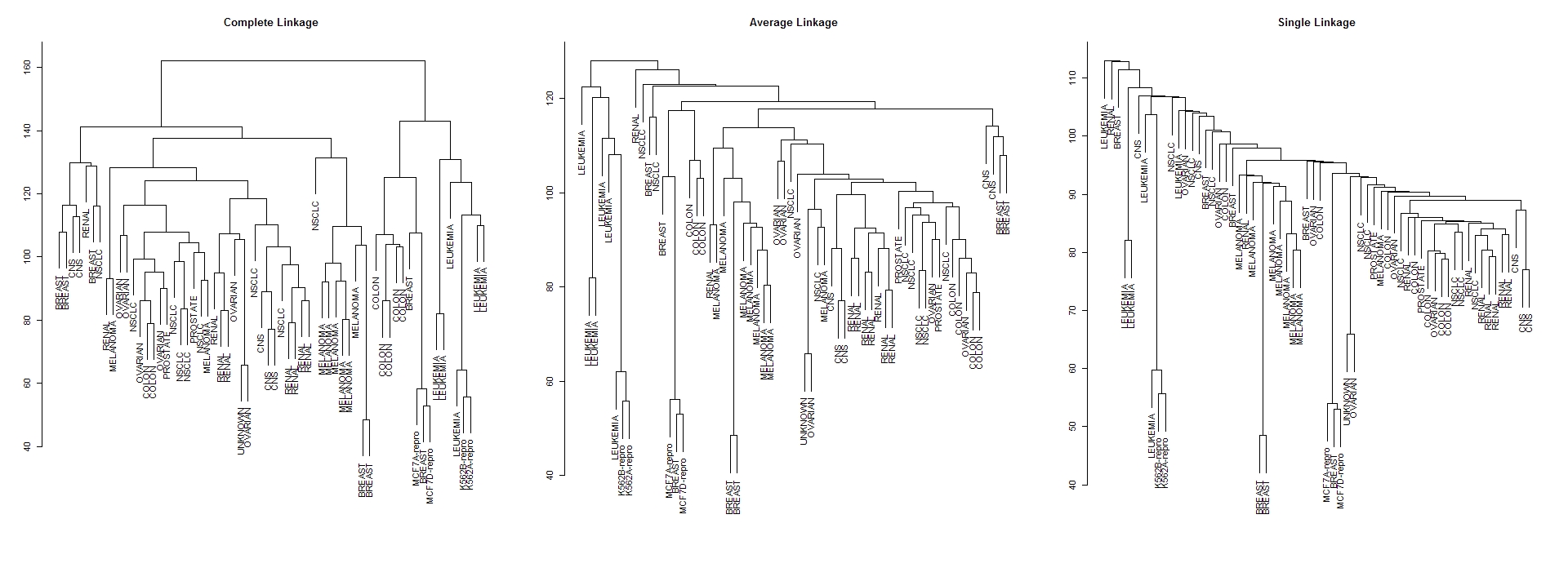
"---------------------- 对癌症的基因表现进行聚类分析 ----------------------"

sc.data <- scale(nci.data)

# 进行系统聚类并绘制谱系图
par(mfcol=c(1,3))
data.dist <- dist(sc.data)
plot(hclust(data.dist), labels=nci.labs, 
     main='Complete Linkage', xlab='', sub='', ylab='')
plot(hclust(data.dist, method='average'), labels=nci.labs, 
     main='Average Linkage', xlab='', sub='', ylab='')
plot(hclust(data.dist, method='single'), labels=nci.labs, 
     main='Single Linkage', xlab='', sub='', ylab='')

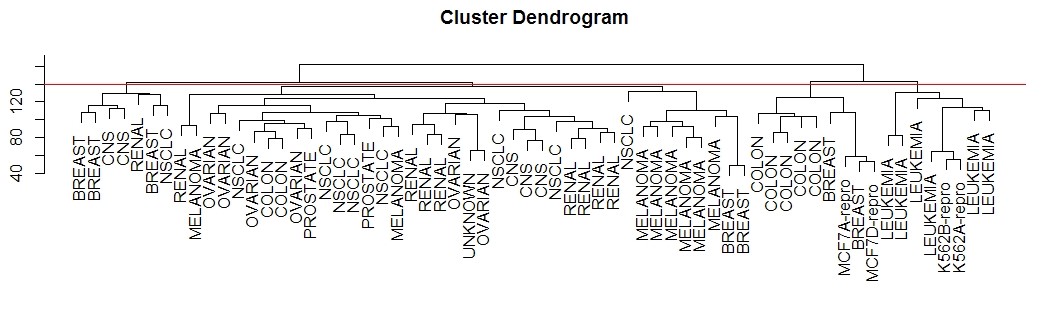
# 在谱系图上某个高度切割可以产生指定类数的聚类，例如 4 类
hc.out <- hclust(dist(sc.data), method='complete')
hc.clusters <- cutree(hc.out, 4)
table(hc.clusters, nci.labs)

# 绘制这四个类的谱系图切割位置
par(mfrow=c(1,1))
plot(hc.out, labels=nci.labs, xlab='', sub='', ylab='')
abline(h=139, col='red')

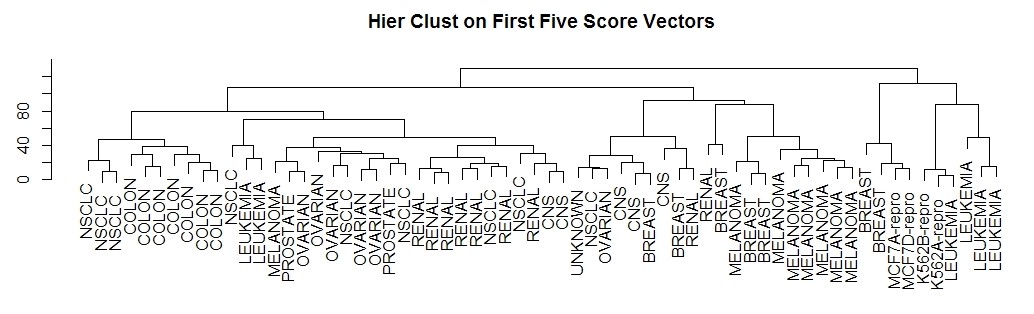
# 只对前几个主成分得分向量进行系统聚类，而不是全部变量
hc.out <- hclust(dist(pr.out$x[, 1:5]))
plot(hc.out, labels=nci.labs, 
     main='Hier Clust on First Five Score Vectors', 
     xlab='', sub='', ylab='')
table(cutree(hc.out, 4), nci.labs)
# 可将主成分获取的操作，看成是一种去噪处理。

END

R 统计学习（ISLR）-- Learning Notes (III)

决策树 | 支持向量机 | 无监督学习

第八章基于树的方法

8.1 决策树的基本原理

8.2 装袋法、随机森林和提升法

8.3 实验：决策树

（1）构建分类树 – Carseats 数据集

（2）构建分类树 – Boston 数据集

（3）装袋法与随机森林

（4）提升法

第九章支持向量机

9.1 最大间隔分类器

9.2 支持向量分类器

9.3 狭义的支持向量机 – 由线性决策边界过渡到非线性

9.4 多分类的SVM

9.5 与逻辑斯谛回归的关系

9.6 实验：支持向量机

（1）支持向量分类器

（2）支持向量机

（3） ROC 曲线（ Receiver Operating Characteristic）

（4）多分类 SVM

第十章无监督学习（unsupervised learning）

10.1 无监督学习的挑战

10.2 主成分分析

10.3 聚类分析方法

10.4 实验

（1）主成分分析

（2）聚类分析

（3）以 NCI60 数据集为例

目录

文章标签

第八章 基于树的方法

8.1 决策树的基本原理

8.2 装袋法、随机森林和提升法

8.3 实验：决策树

（1）构建分类树 – Carseats 数据集

（2）构建分类树 – Boston 数据集

（3）装袋法与随机森林

（4）提升法

第九章 支持向量机

9.1 最大间隔分类器

9.2 支持向量分类器

9.3 狭义的支持向量机 – 由线性决策边界过渡到非线性

9.4 多分类的SVM

9.5 与逻辑斯谛回归的关系

9.6 实验：支持向量机

（1）支持向量分类器

（2）支持向量机

（3） ROC 曲线（ Receiver Operating Characteristic）

（4）多分类 SVM

第十章 无监督学习（unsupervised learning）

10.1 无监督学习的挑战

10.2 主成分分析

10.3 聚类分析方法

10.4 实验

（1）主成分分析

（2）聚类分析

（3）以 NCI60 数据集为例

目录

文章标签

第八章基于树的方法

第九章支持向量机

第十章无监督学习（unsupervised learning）