MATLAB 数据处理方面功能强大,尤其在高维数据处理和矩阵运算方面。隔壁家的 NumPy 和 R 就是个弟弟。并且 Matlab 集成了很多机器学习和数据挖掘算法,图形界面简单上手,懒人福音。缺点就是软件太庞大,只能无事不登三宝殿。在 Linux 中可以通过 matlab -nodesktop -nodisplay 直接在终端运行,Windows 中虽然可以不显示图形界面,但是还是要用 Matlab 自家的 terminal。但是这样可以明显降低内存占用。
科学计算
常用命令
1
2
3
4
5
6
7
8
9
10
11
% 切换数值显示模式
format long e
pi
format short
pi
% 列出工作区变量
who
% 清除工作区变量
clear
% 清屏
clc
数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
% 创建数组
N = []; % 空数组
row = [1 2 3 4]; % 一维行向量
col = [1;2;3;4]; % 一维列向量
square = [1 2 3; 4 5 6; 7 8 9]; % 3x3二维数组
N(1:4) = [2 4 8 16]; % 索引与赋值,索引从 1 开始
% 数组运算
N / row % 左除,得到标量
N ./ row % 点左除,类似元素积,这里是元素商,分母在右
N \ row % 右除,得到矩阵
N .\ row % 点右除,类似元素积,这里是元素商,分母在左
A * B % 矩阵乘
B .* C % 点乘(注意不是数学上的点乘,这里是元素积,求和为点乘结果)
sqrtm(square) % 矩阵平方根,即 sqrtm(X) * sqrtm(X) = X,其中 * 为矩阵乘
sqrt(N) % 分别对每个元素开方
矩阵
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
% 创建矩阵
a = [1 2 3; 4 5 6]
b = [a;7 8 9]
% 索引元素
a(2, 2) % 值为5的元素
b(1, :) % 第一行
b(:, 2) % 第二列
b(2:3, 2:3) % 一个2x2的子块:[5 6; 8 9]
% 矩阵生成函数
c = zeros(3) % 3x3全零
c = ones(3) % 3x3全一
c = eye(3) % 3x3对角矩阵
% 矩阵运算
b / c % 左除
b \ c % 右除
% 对于两个方阵,左除和右除是对称的:b/c=c\b
% 非方阵结果不一致,可能有error或warning,这里不完全遵循数学上的运算法则
[e1, e2] = eig(a) % 得到方阵的特征向量和特征值
[L, U, P] = lu(a) % LU分解
多项式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
% 生成多项式
poly2sym([1 2 3 4]) % 参数为系数,幂数由高到低直到零次
poly2sym(poly(b)) % 由矩阵求特征多项式
root = [-5 -3+4i -3-4i] % 定义一个特征根
poly2sym(poly(root)) % 由特征根生成多项式
% 多项式的运算
p=[1 11 55 125];
b=[1 1;1 1];
polyval(p,b)
polyvalm(p,b)
p=[2 -5 6 -1 9];
roots(p) %求对应系数的多项式的所有根
c=[ 10 40 100 160 170 120];
u=[1 2 3 4];
[q,r]=deconv(c,u) %计算多项式c/u
poly2sym(p)
Dp=polyder(p) %求多项式微分
poly2sym(Dp)
代数与微积分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
% 定义代数式
U=sym('3*x^2+5*y+2*x*y+6') %定义符号表达式
syms x y %建立符号变量
V=3*x^2+5*y+2*x*y+6 %定义符号表达式V
2*U-V+6 %由已知代数式计算新的代数式
% 代数运算
A=sym('[a,2*b;3*a,0]') % 由行列式创建方程组
transpose(A) %转置
factor(U) %分解因式
simplify(U) %自动化简
syms a x; f=sin(a*x) %创建函数f
dfx=diff(f,x) %对x求导
dfa=diff(f,a) %对a求导
f1=x*log(1+x) %创建函数f1
int1=int(f1,x) %求x的不定积分
int2=int(f1,x,0,1) %0-1区间上的定积分
%求微分方程dy/dx+3xy=xe^(-x^2)的通解:
f1=dsolve('Dy+3*x*y=x*exp(-x^2)','x')
%求微分方程在y|x=1 = 2e初始条件下的特解:
f2=dsolve('x*Dy+2*y-exp(x)=0','y(1)=2*exp(1)','x')
%求二阶微分方程的通解:
f3=dsolve('D2y+2*Dy+exp(x)=0','x')
数据可视化
基本绘图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
% 自变量(创建序列)
x = -2*pi:pi/100:2pi
% 工作区绘图:选中工作区变量,点击菜单栏【绘图】选项卡,选择图形
% 命令绘图:plot(x1, y1, option1, x2, y2, option2, ...)
% 获取相应绘图指令:help graph3d(包名)
% 三维绘图:plot(x1, y1, z1, option1, x2, y2, z2, option2, ...)
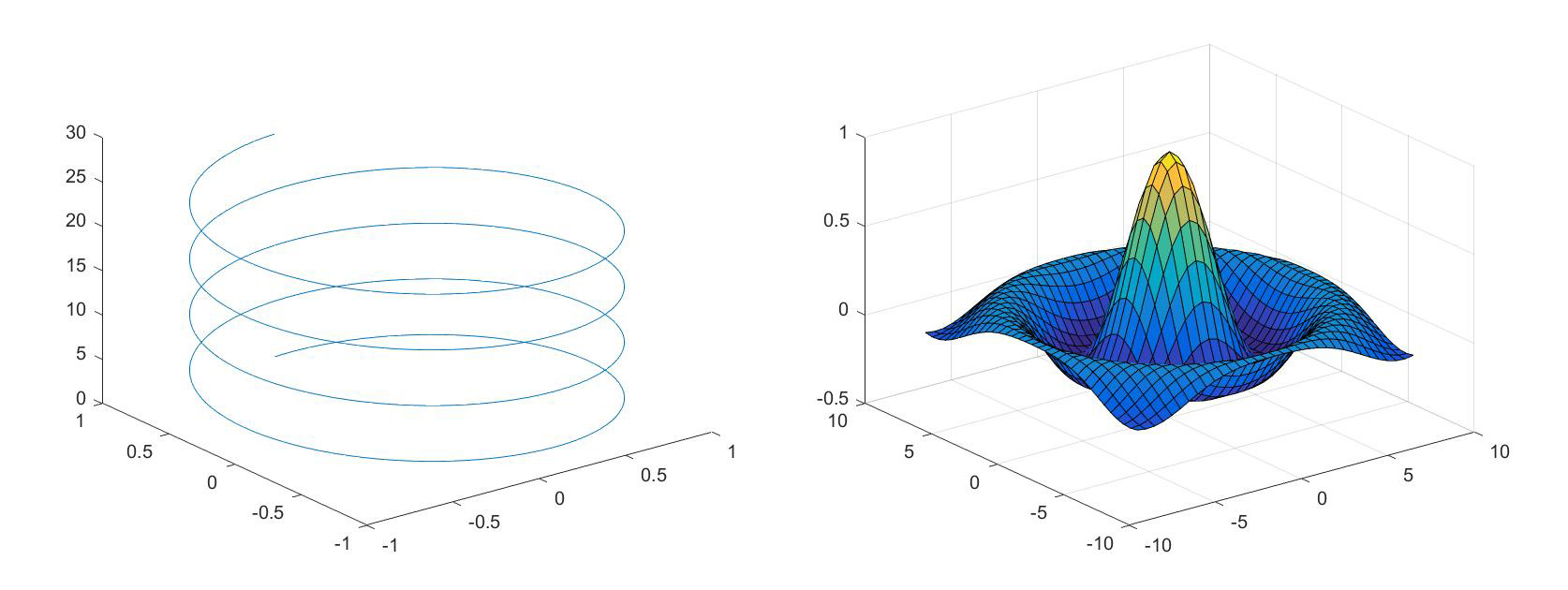
% 示例1:三维曲线
t = 0:pi/50:8*pi;
x = sin(t); y = cos(t); z = t;
plot3(x, y, z)
% 示例2:三维曲面
x = -8:0.5:8; y = x;
[X, Y] = meshgrid(x, y); % 设置矩形网格
R = sqrt(X.^2 + Y.^2) + eps;
Z = sin(R) ./ R; % 定义函数关系
mesh(X, Y, Z) % 绘制曲面网格
grid on % 坐标空间网格
surf(X, Y, Z) % 绘制曲面阴影
图像修饰
1
2
3
4
5
6
7
8
9
10
11
12
13
% 打开不同的图形窗口:figure(1), figure(2), ...
% 划分图形窗口:subplot(m, n, p) -- 分成m*n的窗格,p为当前子图编号
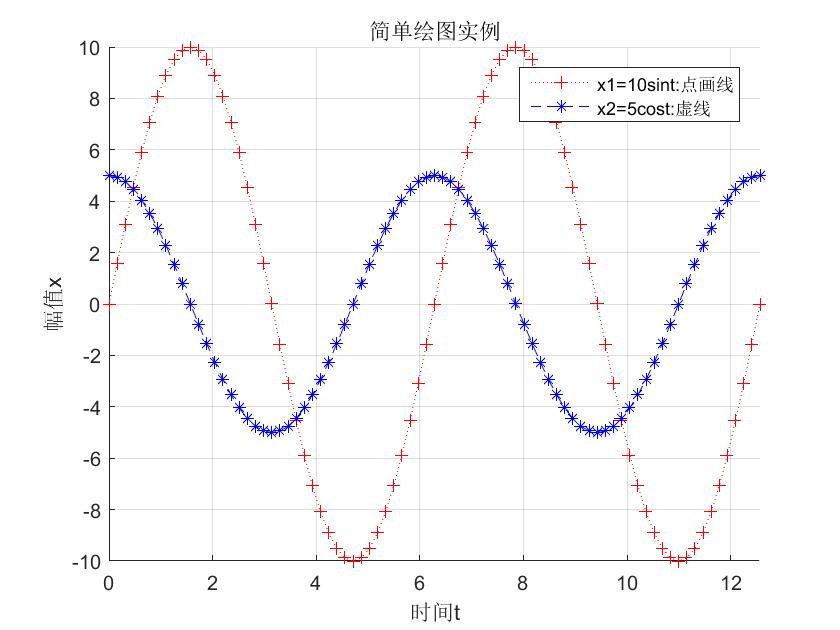
% 示例
t=[0:pi/20:4*pi];
hold on %允许在同一坐标系上绘制多个图形
axis([0 4*pi -10 10]) %设置坐标轴范围
plot(t,10*sin(t),'r+:') %线形为点画线,颜色为红色,数据点为加号形状
plot(t,5*cos(t),'b*--')
xlabel('时间t'); ylabel('幅值x')
title('简单绘图实例')
legend('x1=10sint:点画线','x2=5cost:虚线') %添加文字注释
grid on
计算机视觉应用
图像白化处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
clear, clc, close all;
I = imread('test.png');
[m, n] = size(I);
p = reshape(I, m*n, 1); % 矩阵转为向量
p = single(p); % 转为单精度
mu = mean(p); % 取均值
va = var(p); % 取方差
for i=1:m % 归一化
for j=1:n
X(i,j) = (double(I(i,j))-mu)/sqrt(va);
end
end
figure, imshow(I)
figure, imshow(X)
% 搞来搞去,感觉还是 opencv 好用一点,MatLab不太行啊
% 有空深入学习一下 opencv


CV模型交叉验证例子
———-get_angerr.m———-
1
2
3
4
5
6
7
8
% 输入参数 test:测试值 -- 即真值,三通道颜色矩阵
% 输入参数 pred:对应 test 的预测值
% 输出:预测值和真值的角误差 -- 即高维张量在欧几里得空间的余弦相似度
function [r] = get_angerr(test, pred)
i1 = test / sqrt(sum(test.^2));
i2 = pred / sqrt(sum(pred.^2)); % 尺度缩放
r = acosd(sum(i1(:).^2(:))); % 点积的反余弦
———-grid_search.m———-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
% 导入模型参数表
load('Params_Grid.mat')
% 空矩阵,储存验证集误差
AngularError = zeros(4, N);
idx = 1; % 遍历 N 组参数
best = 1; % 初始化最优参数序号
error = 1e5; % 初始化误差值
% 遍历对应的模型结果
for i = 1:10
for j = 1:10
for k = 1:10 % 循环范围取决于参数网格精度
% 根据参数导入对应模型结果
eval(['load(', num2str(i), num2str(j), num2str(k), '.mat);']);
% 计算并储存误差度量值
AngularError(1, idx) = get_angerr(y_dev, y_pred);
AngularError(2, idx) = i; %储存参数 i
AngularError(3, idx) = j; %储存参数 j
AngularError(4, idx) = k; %储存参数 k
idx = idx + 1;
% 更新最优参数序号
if AngularError(1, idx) < error
error = AngularError(1, idx);
best = idx
end
end
end
end
这里只作为 matlab 流程控制和函数功能的示例,实际上交叉验证使用自带的函数就可以完成。