部分公式在 GitHub Pages 上渲染有问题，请在 Gitee Pages 阅读本文

CHPT01 – 随机事件与概率

一、 随机现象与随机试验

随机试验：

• 试验可以在相同的条件下重复进行
• 试验可能出现的所有结果种类已知
• 试验结果在试验前未知，但必是所有可能结果中的一个

随机事件： 随机试验的结果

随机现象： 随机试验中观察到的现象

统计规律性： 在随机试验的重复实施中呈现的不变性质

（1）样本空间与随机事件

样本空间： 随机试验所有可能结果的集合；用 $\Omega$ 表示

• 有限样本空间：有限个元素，如抛硬币的结果
• 无限样本空间：无限个元素，如灯泡的寿命

样本点： 样本空间的元素；用 $\omega$ 表示

事件的发生： 当 $\omega\in{A}$ ，称这次试验中事件 A 发生；当 $\omega\notin{A}$ ，称事件 A 不发生；

两种特殊的随机事件：

• 必然事件：事件样本空间在每次实验中都发生
• 不可能事件：空集 $\Phi$ 在每次实验中均不发生，称为不可能事件

基本事件： 只含单个样本点的集合，称为基本事件，或称简单事件

• 不能再分解的事件称为基本事件
• 由基本事件组合而成的事件称为复合事件
• 基本事件是相对的，不是绝对的

（2）事件的关系与运算

事件的关系：

• 事件的包含：如果事件 A 发生，则事件 B 一定发生，则称事件 B 包含事件 A；记为：$A\subset{B}$；根据定义显然有：$A\subset\Omega$。
• 事件的相等：如果事件 A 与事件 B 互相包含，即 ${A}\subset{B}$ 且 ${B}\subset{A}$，则称事件 A 等于事件 B；记为：${A}={B}$。
• 事件的互斥：如果事件 A 与事件 B 不能在同一次试验中都发生（但可以都不发生），则称事件 A 与事件 B 是互斥或互不相容的；记为：${A}\cap{B}=\Phi$。
• 事件的对立：如果事件 A 与事件 B 不同时发生，但必发生一个，则称事件 A 与事件 B 为对立事件；记为：$B=\overline{A},\ {A}=\overline{B}$； 根据定义显然有：${AB}=\Phi,\ {A}+{B}=\Omega$。

事件的运算：

• 和：$A\cup{B}$ （并集）
  • 当 A、B 互斥时，可记为 ${A}+{B}$
  • 当 $A_1,\ A_2,\ …,\ A_n$ 两两互斥时，可记为 $\bigcup_{i=1}^{n}A_i=\sum_{i=1}^{n}A_i$
  • 当 $A_1,\ A_2,\ …,\ A_n$ 两两互斥，且 $A_1+A_2+…+A_n=\Omega$，则称这 n 个事件构成互斥完备群
• 积：$A\cap{B}$ 或 ${AB}$ （交集）
  • 可列多个事件的积事件记为 $\prod_{i=1}^{\infty}A_i$，表示一系列事件全部发生
• 差： ${A-B}$ 或 ${A}\backslash{B}$ （指 A 发生，B 不发生）
  • 由定义有：${A-B}={A}\cap\overline{B},\ {A}=\Omega-\overline{A}$

事件的运算法则：

• 交换律：$A\cup{B}={B}\cup{A},\ AB=BA$
• 结合律：$\left({A}\cup{B}\right)\cup{C}={A}\cup\left({B}\cup{C}\right),\ \left(AB\right)C=A\left(BC\right)$
• 分配律：
  • $A\cap\left({B}\cup{C}\right)=\left(A\cap{B}\right)\cup\left(A\cap{C}\right)$
  • ${A}\cup\left({B}\cap{C}\right)=\left(A\cup{B}\right)\cap\left(A\cup{C}\right)$
• 对偶律：
  • $\overline{A\cup{B}}=\overline{A}\cap\overline{B},\ \ \ \ \overline{A\cap{B}}=\overline{A}\cup\overline{B}$
  • $\overline{\bigcup_{i=1}^n{A_i}}=\bigcap_{i=1}^n\overline{A_i}, \ \ \ \ \overline{\bigcap_{i=1}^n{A_i}}=\bigcup_{i=1}^n\overline{A_i}$

二、概率的定义

（1）概率的统计定义

频率：设事件 A 在 n 次试验中出现了 r 次，则比值 r/n 称为事件 A 在 n 次试验中出现的频率

概率的统计定义：在同一组条件下所作的大量重复试验中，事件 A 出现的频率总是在区间 [0, 1] 上的一个确定的常数 p 附近摆动，并且稳定于 p ，则 p 称为事件 A 的概率，记作 $P\left(A\right)$

（2）概率的古典定义

古典概型随机试验：

• 有限性：只有有限多个不同的基本事件
• 等可能性：每个基本事件出现的可能性相等

古典概率：在古典概型中，如果基本事件（样本点）的总数为 n，事件 A 所包含的基本事件（样本点）个数为 r (r≤n)，则定义事件 A 的概率 $P\left(A\right)=r/n$。即：

（3）概率的几何定义

几何概型随机试验：平面上有可测的区域 G 和 g（g 包含在 G 内），向 G 中随机投掷一点 M，设 M 必落在 G 内。如 M 落在 g 内的概率只与 g 的面积成正比，而与 g 的位置和形状无关。这样的随机实验，称为几何概型。

几何概率： $P={g\ 的面积}\ /\ {G\ 的面积}\ $

（4）概率的公理化定义

前三种概率定义的局限性：

• 古典概型：实验结果要求有限、互不相容、等可能性
• 几何概型：要求落入任何一点的概率等可能
• 统计概型：要求大量重复试验

事件域：由样本空间的一些子集构成的集合 $F$，如果满足以下条件，则称 $F$ 为一个事件域。$F$ 中的元素称为随机事件，$\Omega$ 为必然事件，$\Phi$ 为不可能事件。

• $\Omega\in{F}$
• $if\ A\in{F},\ then\ \overline{A}\in{F}$
• $if\ A_n\in{F},\ n=1,2,…,\infty;\ then\ \bigcup_{n=1}^{\infty}A_n\in{F}$

概率的公理化定义：设 $\Omega$ 为样本空间，$A\in{F}$，$P\left(A\right)$ 是 $A$ 的实值函数，且满足以下三条公理，则称 $P\left(A\right)$ 是事件 $A$ 的概率。$P$ 称为事件域 $F$ 上的概率测度。

• 公理1：对于任一事件 $A$ 有：$0\leq{P}\left(A\right)\leq{1}$
• 公理2：$P\left(\Omega\right)=1$
• 公理3：对于可列多个两两互斥的事件 $A_1,A_2,…,A_n,…$，有 $P\left(\bigcup_{i=1}^{\infty}A_i\right)=\sum_{i=1}^{\infty}P\left(A_i\right)$

概率的性质：

1. 非负性：对于任一事件 A 有：$0\leq{P}\left(A\right)\leq{1}$
2. 规范性：$P\left(\Omega\right)=1$
3. 可加性：若事件 A 与 B 互斥，则 $P\left(A+B\right)=P\left(A\right)+P\left(B\right)$
4. $P\left(\Phi\right)=0$
5. $if\ A\subset{B},\ then\ P\left(A\right)\leq{P}\left(B\right)$
6. $对任意\ A，有\ P\left(\overline{A}\right)=1-P\left(A\right)$
7. $对任意\ A和B，有\ P\left(B\backslash{A}\right)=P\left(B\right)-P\left(AB\right)$
8. $对任意\ A和B，有\ P\left(A\cup{B}\right)=P\left(A\right)+P\left(B\right)-P\left(AB\right)$
9. 上连续性：$if\ A_1\subset{A_2}\subset{…}\subset{A_n}\subset{…},\ then\ P\left(\bigcup_{i=1}^{\infty}A_i\right)=\lim_{n\rightarrow\infty}P\left(A_n\right)$
10. 下连续性：$if\ A_1\supset{A_2}\supset{…}\supset{A_n}\supset{…},\ then\ P\left(\bigcap_{i=1}^{\infty}A_i\right)=\lim_{n\rightarrow\infty}P\left(A_n\right)$

三、条件概率与独立性

（1）条件概率

条件概率：对事件 A、B，若 $P\left(B\right)>0$，则称 $P\left(A|B\right)=\frac{P\left(AB\right)}{P\left(B\right)}$ 为事件 A 在 事件 B 发生下的条件概率。

条件概率的性质：

• 非负性：对于任意事件 B，必有 $P\left(B|A\right)\geq{0}$
• 规范性：若 $B\subset{A}$，则 $P\left(A|B\right)=1$
• 可加性：若 $B_1,B_2,…,B_n,…$ 为一系列两两互不相容事件，则 $P\left(\sum_{k=1}^{\infty}B_k|A\right)=\sum_{k=1}^{\infty}P\left(B_k|A\right)$

（2）乘法公式

定理1：

$if\ P\left(A\right)>0,\ then\ P\left(AB\right)=P\left(A\right)P\left(B|A\right)$

一般地：

$if\ P\left(A_1{A_2}…A_{n-1}\right)>0$

$then\ P\left(A_1{A_2}…A_n\right)=P\left(A_1\right)P\left(A_2|A_1\right)P\left(A_3|A_1{A_2}\right)…P\left(A_n|A_1{A_2}…A_{n-1}\right)$

（3）全概率公式与贝叶斯公式

定理（全概率公式）：设 $B_1,B_2,…,B_n$ 是一组两两互斥的事件，且 $\sum_{i=1}^{n}B_i=\Omega$, $P\left(B_i\right)>0\ \ \ \ i=1,2,…,n$，则对任一事件 $A$ 都有：

定理（贝叶斯公式）：设 $B_1,B_2,…,B_n$ 是一组两两互斥的事件，且 $\sum_{i=1}^{n}B_i=\Omega$, $P\left(B_i\right)>0\ \ \ \ i=1,2,…,n$，则对任一具有正概率的事件 $A$ 都有：

（4）事件的独立性

定义：若两事件 A、B 满足 $P\left(AB\right)=P\left(A\right)P\left(B\right)$，则称事件 A、B 相互独立。由定义有：

• 在 $P\left(A\right)=0$ 或 $P\left(A\right)=0$ 时仍然适用
• 必然事件以及不可能事件与任意事件相互独立
• 当 $P\left(A\right)>0$ 时有：事件 A、B 相互独立 $\Leftrightarrow$ $P\left(B|A\right)=P\left(B\right)$
• 当 $P\left(B\right)>0$ 时有：事件 A、B 相互独立 $\Leftrightarrow$ $P\left(A|B\right)=P\left(A\right)$
• $A,B;\ A,\overline{B};\ \overline{A},B;\ \overline{A},\overline{B}$ 这四对事件要么全都相互独立，要么都不相互独立

CHPT02 – 一维随机变量及其分布

一、随机变量的概念及其分布函数

（1）随机变量的概念

定义：称定义在样本空间 $\Omega$ 上的实函数 $X=X\left(\omega\right),\ \omega\in\Omega$ 为随机变量。如对任意实数 $x$，集合 ${\omega|X\left(\omega\right)\leq{x}}$ 都是一随机事件。

（2）一维随机变量的分布函数

定义：设 $X$ 是一个随机变量，$x$ 是任意实数，函数 $F_X\left(x\right)=P\left(\omega|X{\omega\right)\leq{x}}$ 称为随机变量 $X$ 的分布函数，简记为 $F\left(x\right)=P\left(X\leq{x}\right)$。如果某实函数具有以下三个性质，则可作为某随机变量的分布函数。

• $if\ x_1<x_2,\ then\ F\left(x_1\right)\leq{F}\left(x_2\right)$
• $0\leq{F}\left(x\right)\leq{1}$
• 右连续性：对任意实数 $x_0$ 有 $F\left(x_0+0\right)=F\left(x_0\right)$，其中 $F\left(x_0+0\right)=\lim_{x\rightarrow{x_0^{+}}}F\left(x\right)$

二、一维离散型随机变量

离散型随机变量：随机变量的取值只有有限个或可列多个 分布列：设离散型随机变量 $X$ 的全部取值为 $x_1,x_2,…,x_n,…$，且 $P\left(X=x_i\right)=p_i,\ i=1,2,…$，则称上式为 $X$ 的概率分布律，对应取值列表为分布列。显然有：$p_i\geq{0},\ \sum_{i=1}^{\infty}p_i=1$。

（1）二项分布

二项分布：如果一个随机变量 $X$ 取值为 $0,1,2,…,n$，且 $P\left(X=k\right)=C_n^k{p^k}q^{n-k}$，其中 $q+p=1,\ k=1,2,…,n$，则称 $X$ 服从二项分布，记为 $X\sim{B}\left(n,p\right)$

两点分布：$n=1$ 时的二项分布成为两点分布，其分布列为：$\begin{pmatrix} 1 & 0 \ p & q \end{pmatrix}$

单点分布（退化分布）：当随机变量取值为常量 $C$，为单点分布

定理 1：当 $X\sim{B}\left(n,p\right)$，有以下结论：

• 事件 $A$ 发生的次数 $x$ 在 $[k_1,k_2]$ 之间的概率为：$P\left(k_1\leq{x}\leq{k_2}\right)=\sum_{k=k1}^{k_2}b\left(k;n,p\right)$
• 事件 $A$ 发生的次数 $x$ 至少为 $r$ 的概率为：$P\left(x\geq{r}\right)=1-\sum_{k=0}^{r-1}b\left(k;n,p\right)$
• 事件 $A$ 发生的次数 $x$ 至少为 $1$ 的概率为：$P\left(x\geq{1}\right)=1-b\left(0;n,p\right)=1-q^n$

定理 2：设 $X\sim{B}\left(n,p\right)$，令 $m=Int\left[\left(n+1\right)p\right]$，则 $k=m$ 时，$b\left(k;n,p\right)$ 的值最大。若 $\left(n+1\right)p$ 为整数，则 $b\left(m;n,p\right)=b\left(m-1;n,p\right)$。

Python 代码示例：验证定理 2（使用 Numpy）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import math
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

# 计算组合数：
def c(n, m):
    n_ = math.factorial(n)
    m_ = math.factorial(m)
    n_sub_m_ = math.factorial(n-m)
    return int(n_ / (n_sub_m_ * m_))
# 二项分布函数
def b(k, n, p):
    if k >= n:
        return 0
    else:
        return c(n, k) * p**k * (1-p)**(n-k)
# X ~ B(n, p)
n=9; p=0.3; max_ = 'k=2, 3'
# 使用 numpy 中的样本函数采样，模拟分布
sample = np.random.binomial(n, p, 10000)
# plt.hist(sample, align='left', bins=20)
hist = pd.Series(sample).value_counts()
plt.bar(hist.index, hist)
# 使用分布函数计算精确的分布
k = np.arange(15)
Fx = np.array([b(i, n, p) for i in k])
plt.plot(k, Fx*10000, color='brown')    # 同步双轴，忽略坐标刻度问题
plt.title(
    r'$X\sim{B}\left(9,0.3\right),\ \left(n+1\right)p=3$' + 
    f'\tmax {max_}'
)
plt.show()

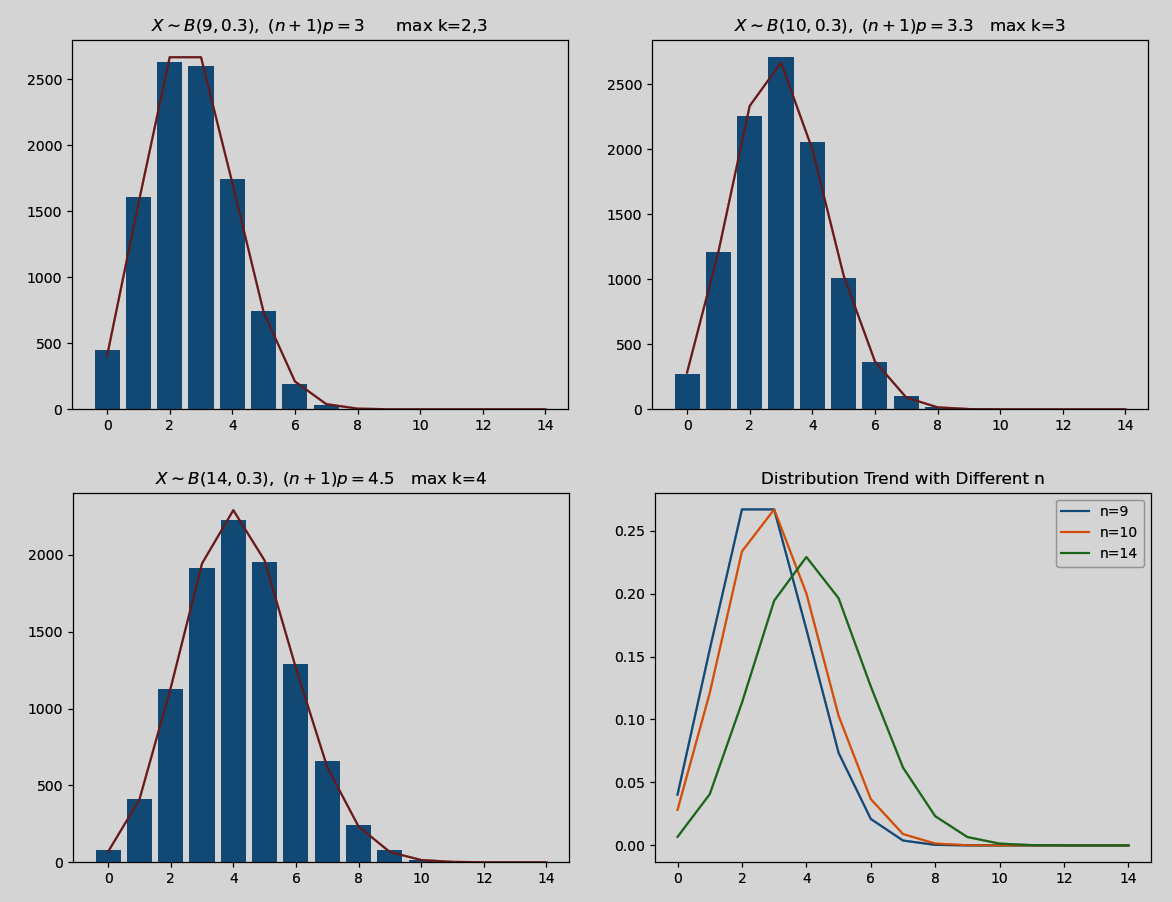
更多的分布函数和随机变量模拟可使用 Scipy 专用统计模块：https://docs.scipy.org/doc/scipy/reference/tutorial/stats.html

（2）泊松分布

泊松分布：若离散型随机变量 $X$ 的分布律为 $P{X=k}=\frac{\lambda^k}{k!}e^{-\lambda}\ \ \ \ k=0,1,2,…$，其中 $\lambda>0$ 是常数，则称 $X$ 服从泊松分布。记为 $X\sim{Pios\left(\lambda\right)}$。

泊松定理：设随机变量 $X$ 服从二项分布 $X\sim{B}\left(n,p_n\right)\ \ \ \ n=1,2,…$，其中概率 $p_n$ 与 $n$ 有关，并且满足 $\lim_{n\rightarrow{\infty}}np_n=\lambda>0$，则有：

泊松分布是二项分布的极限分布：当 $n\rightarrow\infty$，二项分布趋向于 $\lambda=np$ 的泊松分布（当 $n\geq{10},\ p\leq{0.1}$ 时即可近似）

（3）几何分布

几何分布：在“成功”概率是 p 的伯努利试验中，若以 X 记“首次出现成功”所需的试验次数，则 X 服从几何分布：

超几何分布：在 $N$ 个总体中有 $M$ 个目标个体，从中抽取 $n,\ (n\leq{M})$ 件，其中有 $\xi$ 个目标个体的概率分布：

负二项分布：在“成功”概率是 p 的伯努利试验中，出现第 $r$ 次“成功”时所作的试验次数 $\xi$ 服从负二项分布：

三、一维连续型随机变量

定义：设随机变量 $X$ 的分布函数为 $F\left(x\right)$，若存在非负函数 $f\left(x\right)$，使得对一切实数 $x$，关系式 $F\left(x\right)=\int_{-\infty}^{x}f\left(x\right)dt$ 都成立，则称 $X$ 为连续型随机变量，$f\left(x\right)$ 称为 $X$ 的密度函数。

性质：

• $f\left(x\right)\geq{0}$
• $\int_{-\infty}^{+\infty}f\left(x\right)dx=1$
• $P{a<X\leq{b}}=F\left(b\right)-F\left(a\right)=\int_{a}^{b}f\left(x\right)dx$
• 若 $f\left(x\right)$ 在点 $x$ 的某邻域内连续，则有 $F’\left(x\right)=f\left(x\right)$

（1）均匀分布

设 $a,b$ 为有限数，且 $a<b$。如果随机变量 $X$ 分布密度为：

则称 $X$ 在 $[a,b]$ 上服从均匀分布，记作 $U\left(a,b\right)$。对应的分布函数为：

（2）指数分布

$X\sim{Exp\left(\lambda\right)}$，$\lambda>0$ 为常数，其分布密度：

分布函数：

（3）正态分布

$X\sim{N\left(\mu,\sigma^2\right)}$，$\mu,\sigma>0$ 为常数，其分布密度：

分布函数：

特别地，称 $X\sim{N(0,1)}$ 为标准正态分布。

CHPT03 – 随机向量及其分布

一、随机向量的概念及其分布函数

（1）二维随机向量及其分布

定义 1：设 $\left(\Omega,F,P\right)$ 为概率空间，如果 $X_i,\ i=1,2,…,n$ 为随机变量，则称向量 $\left(X_1,X_2,…,X_n\right)$ 为随机向量。

定义 2：设 $(X,Y)$ 是二维随机变量，对任意实数 $x,y$，函数 $F(x,y)=P{X\leq{x},Y\leq{y}}$ 称为 $(X,Y)$ 的联合分布函数。

定理：设 $F(x,y)$ 为随机向量 $(X,Y)$ 的分布函数，则：

• 单调性：$x_1<x_2\rightarrow{F(x_1,y)}\leq{F(x_2,y)}$, $y_1<y_2\rightarrow{F(x,y_1)}\leq{F(x,y_2)}$
• 右连续：$F(x+0,y)=F(x,y)$, $F(x,y+0)=F(x,y)$
• $F(-\infty,y)=F(x,-\infty)=F(-\infty,-\infty)=0$, $F(+\infty,+\infty)=1$

定义 3：n 维随机向量 设 $\left(\Omega,F,P\right)$ 为概率空间，$\left(X_1,X_2,…,X_n\right)$ 为概率空间上的随机向量，它的联合分布函数定义为：

（2）随机变量的独立性

定义：设 $\left(\Omega,F,P\right)$ 为概率空间，$\left(X_1,X_2,…,X_n\right)$ 为概率空间上的随机向量，满足以下条件则称 $X_1,X_2,…,X_n$ 相互独立：

二、二维离散型随机向量的分布律

（1）联合分布律

若随机向量 $(X,Y)$ 所有可能取值是可列多对 $(x_i,y_j),\ i,j=1,2,…$，则称 $(X,Y)$ 是二维离散型随机变量。设 $P{X=x_i,Y=y_j}=p_{ij},\ i,j=1,2,…$，则 $p_{ij}$ 称为 $(X,Y)$ 的联合概率分布律。

（2）边缘分布律

（3）条件分布律

当 $p_{\bullet{j}}>0$ 时，在 $Y=y_j$ 条件下 $X$ 的条件分布律：

当 $p_{i\bullet}>0$ 时，在 $X=x_i$ 条件下 $Y$ 的条件分布律：

三、二维连续型随机向量的分布密度

（1）分布密度函数

定义：对于随机向量 $(X,Y)$，若存在函数 $f(x,y)\geq{0},\ (x,y\in{\mathbb{R}})$，使得 $(X,Y)$ 的分布函数：

则称 (X,Y) 是二维连续型随机向量，$f(x,y)$ 称为 $(X,Y)$ 的密度函数。

性质：

• $f(x,y)\geq{0}$
• $\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}{f(u,v)}dudv=F(+\infty,+\infty)=1$
• 若 $f(x,y)$ 在点 $(x,y)$ 处连续，则 $f(x,y)=\frac{\partial^{2}F(x,y)}{\partial{x}\partial{y}}$
• 若 $\mathbb{D}$ 是 $xOy$ 平面内任一区域，则：$P{(X,Y)\in{\mathbb{D}}}=\iint_{\mathbb{D}}f(x,y)dxdy$

（2）边缘分布密度函数

设连续型随机向量 $(X,Y)$ 的密度函数为 $\varphi(x,y)$，则 (X,Y) 关于 $X$ 的边缘分布函数 $F_{X}(x)$ 有：

其分量 $X$ 是一维连续型随机变量，且 $X$ 的分布密度为：

同理有：

$\varphi_{X}(x),\ \varphi_{Y}(y)$ 分别称为随机向量 $(X,Y)$ 关于 $X, Y$ 的边缘分布密度。

（3）条件分布密度函数

设 $(X,Y)$ 的联合密度为 $f(x,y)$，边缘密度为 $\varphi_{X}(x),\ \varphi_{Y}(y)$。如 $\varphi_{Y}(y)>0$，则：$\varphi(x|y)=\frac{\varphi(x,y)}{\varphi_{Y}(y)}$；如 $\varphi_{X}(x)>0$，则：$\varphi(y|x)=\frac{\varphi(x,y)}{\varphi_{X}(x)}$。

CHPT04 – 随机变量的数字特征

一、一维随机变量的数字特征

（1）随机变量的数学期望

离散型随机变量的数学期望：当 $\sum_{k}\vert{x_k}\vert{p_k}<+\infty$，随机变量存在数学期望：$EX=\sum_{k}x_k{p_k}=\sum_{k}x_k{P(X=x_k)}$

• $X\sim{B(n,p)},\ EX=np$
• $X\sim{Pois(\lambda)},\ EX=\lambda$
• $P\left(X=k\right)=q^{k-1}p,\ EX=1/p$ （几何分布）
• $P\left(\xi=k\right)=\frac{C_{M}^{k}C_{N-M}^{n-k}}{C_{N}^{n}},\ E\xi=\frac{nM}{N}$ （超几何分布）

连续型随机变量的数学期望：当随机变量 $X$ 有概率密度函数 $f(x)$，并且积分 $\int_{-\infty}^{+\infty}\vert{x}\vert{f(x)}dx$ 收敛，则随机变量存在数学期望：$EX=\int_{-\infty}^{+\infty}xf(x)dx$

• $X\sim{U(a,b)},\ EX=\frac{a+b}{2}$
• $X\sim{Exp\left(\lambda\right)},\ EX=1/\lambda$
• $X\sim{N(\mu,\sigma^2)},\ EX=\mu$

（2）随机变量的方差

定义：随机变量 $X$，若 $E(X-EX)^2$ 存在，则记方差为 $Var[X]=DX=E(X-EX)^2$，记标准差为 $\sqrt{Var[X]}$。又由数学期望的性质，可导出方差的另一计算公式：

常见随机变量的方差：

• $X\sim{B(n,p)},\ Var[X]=npq$
• $X\sim{Pois(\lambda)},\ Var[X]=\lambda$
• $P\left(X=k\right)=q^{k-1}p,\ Var[X]=q/p^2$ （几何分布）
• $P\left(\xi=k\right)=\frac{C_{M}^{k}C_{N-M}^{n-k}}{C_{N}^{n}},\ Var[\xi]=\frac{nM}{N}(1-\frac{M}{N})\frac{N-n}{N-1}$ （超几何分布）
• $X\sim{U(a,b)},\ Var[X]=\frac{1}{12}(b-a)^2$
• $X\sim{Exp\left(\lambda\right)},\ Var[X]=1/\lambda^2$
• $X\sim{N(\mu,\sigma^2)},\ Var[X]=\sigma^2$

（3）随机变量的矩

定义：设 $X$ 为随机变量，$c$ 为常数，$k$ 为正整数，如 $E[\vert{x-c}\vert^k]<\infty$，则：$E[(X-c)^k]$ 称为 $X$ 关于 $c$ 点的 $k$ 阶矩。

• 当 c=0 时，$a_k=EX^k$ 称为 $X$ 的 k 阶原点矩；期望是一阶原点矩
• 当 c=EX 时，$\mu_k=E[(X-EX)^k]$ 称为 $X$ 的 k 阶中心矩；方差是二阶中心矩

二、随机向量的数字特征

（1）二维随机向量的协方差

定义：二维随机向量 $(X,Y)$，其协方差定义为：$Cov(X,Y)=E(X-EX)(Y-EY)$。根据定义有：

• $Cov(X,Y)=Cov(Y,X)$
• $Var[X]=Cov(X,X),\ Var[Y]=Cov(Y,Y)$
• $Cov(X,Y)=E(XY)-EXEY$
• $Cov(aX+bY, Z)=aCov(X,Z)+bCov(Y,Z)$
• 若 $X,Y$ 独立，则 $Cov(X,Y)=0$
• $[Cov(X,Y)]^2\leq{Var[X]Var[Y]}$
• $Var[X+Y]=Var[X]+Var[Y]+2Cov(X,Y)$

相关系数：$r(X,Y)$，简记为 $r$，$-1\leq{r}\leq{1}$

相关系数是 $X,Y$ 之间线性相关程度的量度，当 $r=0$ 时表示不线性相关。

（2）条件数学期望

离散型随机变量：如 $p_{i|j}=P{X=x_i|Y=b_j}$，且 $\sum_{i=1}^{\infty}\vert{x_i}\vert{p_{i|j}}<+\infty$，则称：

为 $X$ 在 $(Y=b_j)$ 发生的条件下的条件数学期望。

连续型随机变量：设随机变量 $X$ 在 $(Y=y)$ 发生下的条件密度为 $f_{X|Y}(x|y)$，如 $\int_{-\infty}^{+\infty}\vert{x}\vert{f_{X|Y}(x|y)}dx<+\infty$，则称：

为 $X$ 在 $(Y=y)$ 发生的条件下的条件数学期望。

条件数学期望的性质：

• $if\ a\leq{X}\leq{b},\ then\ a\leq{E}{X|Y=y}\leq{b}$
• $E{aX_1+bX_2|Y=y}=aE{X_1|Y=y}+bE{X_2|Y=y}$
• $E[E(X|Y)]=EX$
• 设 $X,Y$ 为离散型随机变量，则 $EX=\sum_{j=1}^{\infty}P(Y=b_j)E(X|Y=b_j)$

CHPT05 – 大数定律和中心极限定理

一、大数定律

• （弱）大数定律：切比雪夫大数定律、辛钦大数定律、伯努利大数定律
• 强大数定律：柯尔莫哥洛夫强大数定理、博雷尔强大数定理

（1）大数定律定义

马尔科夫不等式：若 $\eta$ 为只取非负值的随机变量，则对任意常数 $\varepsilon>0$ 有：

当 $\eta$ 为连续型随机变量时如下证明：设 $\eta$ 的密度函数为 $f(y)$，当 $y<0$ 时有 $f(y)=0$

切比雪夫不等式：由马尔科夫不等式以及期望和方差的关系，易证得：设随机变量 $X$ 有有限方差，对任意 $\varepsilon>0$，则：

大数定律：设 $X_1,X_2,…,X_n,…$ 是随机变量序列，令 $Y_n=(X_1+X_2+…+X_n)/n$，如存在一个常数序列 ${b_n}$，对任意 $\varepsilon>0$，有 $\lim_{n\rightarrow\infty}P{\vert{Y_n-b_n}\vert\geq\varepsilon}=0$，则称序列 ${X_n}$ 服从大数定律。常数序列常取为 $b_n=EY_n=\frac{1}{n}\sum_{i=1}^{n}EX_i$。

（2）弱大数定律

辛钦大数定律：设 $X_1,X_2,…,X_n,…$ 是独立同分布的随机变量序列，且有有限期望 $\mu$，则对任意 $\varepsilon>0$，有：

显然：$E\left(\frac{X_1+X_2+…+X_n}{n}\right)=\mu$。证明：由切比雪夫不等式可证得。

切比雪夫大数定律：设 $X_1,X_2,…,X_n,…$ 是独立的随机变量序列，且有有限方差，则对任意 $\varepsilon>0$，有：

与辛钦大数定律类似，条件不同。

伯努利大数定律：设 $V_n\sim{B(n,p)}$，其中 $n=1,2,..$，则对任意 $\varepsilon>0$，有：

（3）强大数定律定义

强大数定律：设 $X_1,X_2,…,X_n$ 是独立的随机变量序列，若：

则称 ${X_n}$ 满足强大数定理。

依概率收敛：弱大数定律讨论的是依概率收敛。设有随机变量序列 $X_1,X_2,…,X_n$ 和随机变量 $Y$，若对任意 $\varepsilon>0$，有：

则称随机变量序列 ${X_n}$ 依概率收敛于 $Y$，记为：$X_n\xrightarrow{P}Y$。

以概率 1 收敛：强大数定律讨论的是以概率 1 收敛。设有随机变量序列 $X_1,X_2,…,X_n$ 和随机变量 $Y$，如果：

则称随机变量序列 ${X_n}$ 以概率 1 收敛于 $Y$，记为：$X_n\xrightarrow{a.s}Y$。

（4）强大数定律

柯尔莫哥洛夫不等式：设 $X_1,X_2,…,X_n$ 为独立随机变量序列，具有有限数学期望和方差，则对任意 $\varepsilon>0$，有：

当 $n=1$ 时即为切比雪夫不等式。

柯尔莫哥洛夫强大数定理：（两种条件）设 $X_1,X_2,…,X_n$ 为独立随机变量序列，具有有限的数学期望，且 $\sum_{n=1}^{\infty}\frac{Var[X_n]}{n^2}<+\infty$；或者设 $X_1,X_2,…,X_n$ 为独立同分布随机变量序列，具有有限数学期望；则有：

可记为：$\frac{\sum_{k=1}^{n}X_k}{n}\xrightarrow{a.s}\mu$。

博雷尔强大数定律：

二、中心极限定理

（1）定义

设 $X_1,X_2,…,X_n,…$ 为随机变量序列，具有有限的数学期望和方差。如果：

则称 $X_1,X_2,…,X_n,…$ 服从中心极限定理。

（2）林德伯格-莱维中心极限定理

设 $X_1,X_2,…,X_n,…$ 为独立同分布随机变量序列，$EX_i=\mu>-\infty,Var[X_i]=\sigma^2<+\infty$，令：

则对任意实数 $x$，有：

即当 $n\rightarrow+\infty$，有：$\xi_n\sim{N(0,1)}$。

（3）棣莫弗-拉普拉斯中心极限定理

设 $X_1,X_2,…,X_n,…$ 为独立同分布随机变量序列，$X_i$ 的分布为：

则对任意实数 $x$ 有：

显然，其中 $\sum_{i=1}^{n}X_i\sim{B(n,p)}$。即，设 $Y_n\sim{B(n,p)}$，当 $n\rightarrow+\infty$，有：

（4）验证中心极限定理

首先取任意分布作为总体分布（这里取指数分布，参数 $\lambda=10$），对总体进行抽样，并计算每次抽样的均值：

1
2
3
4
5
6
7
8
9
10
11
import scipy.stats
import numpy as np
import matplotlib.pyplot as plt

def sample_mean(n):
    '''n 为抽样次数'''
    means = []
    for i in range(n):
        samples = np.random.exponential(1/_lambda, N)
        means.append(samples.mean())
    return np.array(means)

根据中心极限定理，样本均值 $\overline{X}$ 的抽样分布服从正态分布 $N(\mu,\sigma^2/n)$，其中 $\mu,\ \sigma^2$ 为总体分布的均值和方差，在这里有 $\mu=1/\lambda=0.1,\ \sigma^2=1/\lambda^2=0.01$。下面对比样本均值的抽样分布和对应的正态分布的密度函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
n = 1000
_lambda = 1; N = 100

sample_means = sample_mean(n)
x = np.linspace(0.5,1.5,1000)
norm_kde = scipy.stats.norm.pdf(x, 1/_lambda, np.sqrt(1/N*_lambda**2))

# 样本均值抽样分布的频数密度
plt.hist(sample_means, 30, density=True, color='blue')
# 对应的正态分布的密度函数曲线
plt.plot(x, norm_kde, color='orange')
plt.title('Central Limit Theorem: ' + r'$\overline{X}\sim{N(\mu,\sigma^2/n)}$')
plt.show()

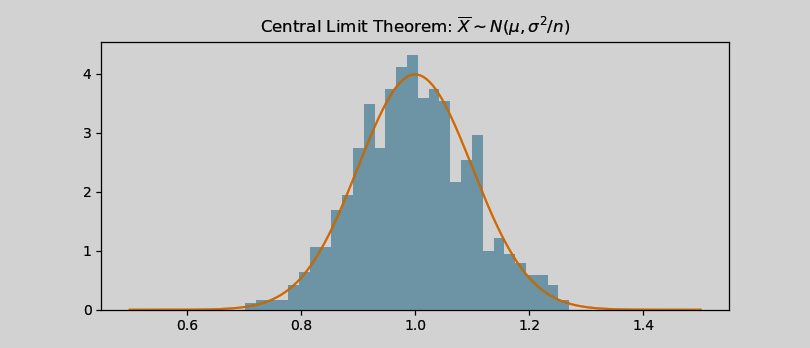
可以看到样本均值的频数分布高度拟合对应的正态分布

• Previous
  Python 处理 PDF 文件
• Next
  概率论与数理统计（下）