CHPT06 – 数理统计基本概念
数理统计:使用概率论和其他数学方法,研究怎样收集(试验和观察)带有随机误差的数据,并在统计模型下对数据进行分析(统计分析),以对所研究的问题作出推断(统计推断)。由于所收集的数据只能反映事物的局部特征,数理统计的任务就在于从统计资料反映的局部特征,以概率论作为理论基础去推断事物的整体特征。区别如下:
- 概率论中通常已知随机变量的分布,然后对其性质以及相互关系推导研究。
- 数理统计中随机变量的分布是未知的,或者已知分布类型而不知道具体参数,需要确定这个随机变量的具体分布。研究方法是归纳法,与概率论相反。
一、总体、样本和统计量
(1)总体与样本
总体:某一问题研究对象的全体
个体:组成总体的单个研究对象
样本:在一个总体中,抽取 n 个个体 $X_1,X_2,…,X_n$,这 n 个个体总称为总体的样本或字样,n 称为样本容量。
简单随机样本:满足以下特性的样本为简单随机样本:
- 代表性:样本中的每一个分量 $X_i\ (i=1,2,…,n)$ 与总体有着相同的分布
- 独立性:n 个样本 $X_1,X_2,…,X_n$ 是相互独立的
命题(样本分布) 对于总体 $X$ 的样本 $X_1,X_2,…,X_n$,若 $X$ 的分布函数为 $F(x)$,那么样本的联合分布函数为 $\prod_{i=1}^{n}F(x_i)$;若 $x$ 的分布密度为 $\varphi(x)$,那么样本的联合分布函数为 $\prod_{i=1}^{n}\varphi(x_i)$。
(2)统计量
含义:样本是总体的反映,但是需要先将样本含有的信息加工浓缩,在统计学中通过构造一个合适的依赖于样本的函数(统计量)来浓缩信息。
定义:设 $X_1,X_2,…,X_n$ 是总体 $\xi$ 的一个样本,若 $g(X_1,X_2,…,X_n)$ 是连续函数,且其中不包含任何未知参数,称样本函数 $g(X_1,X_2,…,X_n)$ 为统计量。
常用统计量:设 $X_1,X_2,…,X_n$ 是总体 $X$ 的一个样本,
- 样本均值:$\overline{X}=\frac{1}{n}\sum_{i=1}^{n}X_i$
- 样本方差:$S_n^2=\frac{1}{n}\sum_{i=1}^{n}(X_i-\overline{X})^2$
- 修正样本方差:$S_n^{*2}=\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\overline{X})^2$
- 样本标准差(均方差):$S_n=\sqrt{\frac{1}{n}\sum_{i=1}^{n}(X_i-\overline{X})^2}$
- 样本 k 阶原点矩:$\overline{X^k}=\frac{1}{n}\sum_{i=1}^{n}X_i^k$
- 样本 k 阶中心矩:$\frac{1}{n}\sum_{i=1}^{n}(X_i-\overline{X})^k$
- 顺序统计量:$X_{(1)}\leq{X_{(2)}}\leq{…}\leq{X_{(n)}}$,即将样本排序
- 样本中位数:当 n 为奇数:$X_{(\frac{n+1}{2})}$;当 n 为偶数:$\frac{1}{2}\left(X_{(\frac{n}{2})}+X_{(\frac{n}{2}+1)}\right)$
- 样本极差:$R_n^X=X_{(n)}-X_{(1)}$
二、经验分布函数
设总体的样本 $X_1,X_2,…,X_n$ 一次样本观测值为 $(x_1,x_2,…,x_n)$,将它们从小到大排序为 $x_{(1)}\leq{x_{(2)}}\leq{…}\leq{x_{(n)}}$,令经验分布函数为:
\[F_n^X\left(x\right)= \left\{ \begin{aligned} \begin{array}{**lr**} 0,\ &x<x_{(1)}\\ \frac{1}{n},\ &x_{(1)}\leq{x}\leq{x_{(2)}}\\ ...\ &\\ \frac{k}{n},\ &x_{(k)}\leq{x}\leq{x_{(k+1)}}\\ ...\ &\\ 1,\ &x\geq{x_{(n)}} \end{array} \end{aligned} \right.\]对于每一个固定的 $X$,$F_n^X(x)$ 是事件 $X\leq{x}$ 发生的频率,当 n 固定时,它是一个随机变量。由伯努利大数定律,当 n 足够大时,$F_n^X(x)$ 依概率收敛于 $X$ 的分布函数 $F_X(x)$。即对于任意给定的 $\varepsilon>0$ 有:
\[\lim_{n\rightarrow\infty}P\left(\bigg|F_n^X(x)-F_X(x)\bigg|\geq\varepsilon\right)=0\]由此可见,当 n 足够大时,经验分布函数是总体分布函数的一个良好近似。
三、抽样分布
统计量的分布称为抽样分布
(1)样本均值和样本方差的数字特征
设 $(X_1,X_2,…,X_n)$ 是取自总体 $X$ 的一个样本,已知 $EX=\mu,\ Var[X]=\sigma^2$,则:
- $E\overline{X}=\mu$
- $Var[\overline{X}]=\frac{\sigma^2}{n}$
- $ES_n^2=\sigma^2$
- $ES_n^{*2}=\frac{n-1}{n}\sigma^2$
(2)三种重要的概率分布
$\chi^2$ 分布:设 $X_1,X_2,…,X_n$ 相互独立,且都服从标准正态分布,则称随机变量 $X=X_1^2+X_2^2+…+X_n^2$ 服从自由度为 $n$ 的卡方分布,记为 $X\sim\chi^2(n)$。卡方分布具有以下性质:
- $EX=n,\ Var[X]=2n$
- 如 $X,Y$ 相互独立,且 $X\sim\chi^2(m),\ Y\sim\chi^2(n)$,则 $X+Y\sim\chi^2(m+n)$
- 当 $n\rightarrow\infty$,有 $\frac{X-n}{\sqrt{2n}}\sim{N(0,1)}$
$t$ 分布:设 $X\sim{N(0,1)},\ Y\sim{\chi^2(n)}$,且它们相互独立,则随机变量 $T=\frac{X}{\sqrt{Y/n}}$ 服从自由度为 $n$ 的 $t$ 分布,记为 $T\sim{t(n)}$。有如下常用性质:
- $t$ 分布的密度函数为偶函数
- $n=1$ 时,$t$ 分布成为 柯西分布;柯西分布不存在任何阶矩
- $n=2$ 时, $ET$ 存在,而 $Var[T]$ 不存在
- $n>2$ 时,$ET=0,\ Var[T]=\frac{n}{n-2}$
- $t$ 分布的极限分布是标准正态分布(n>45即可近似):
$F$ 分布:设 $X\sim{\chi^2(m)},\ Y\sim{\chi^2(n)}$,且相互独立,则随机变量 $Z=\frac{X/m}{Y/n}$ 服从第一自由度为 $m$、第二自由度为 $n$ 的 $F$ 分布,记为 $Z\sim{F(m,n)}$ 常用性质:
- $if\ Z\sim{F(m,n)},\ then\ \frac{1}{Z}\sim{F(n,m)}$
- $if\ X\sim{t(n)},\ then\ X^2\sim{F(1,n)}$
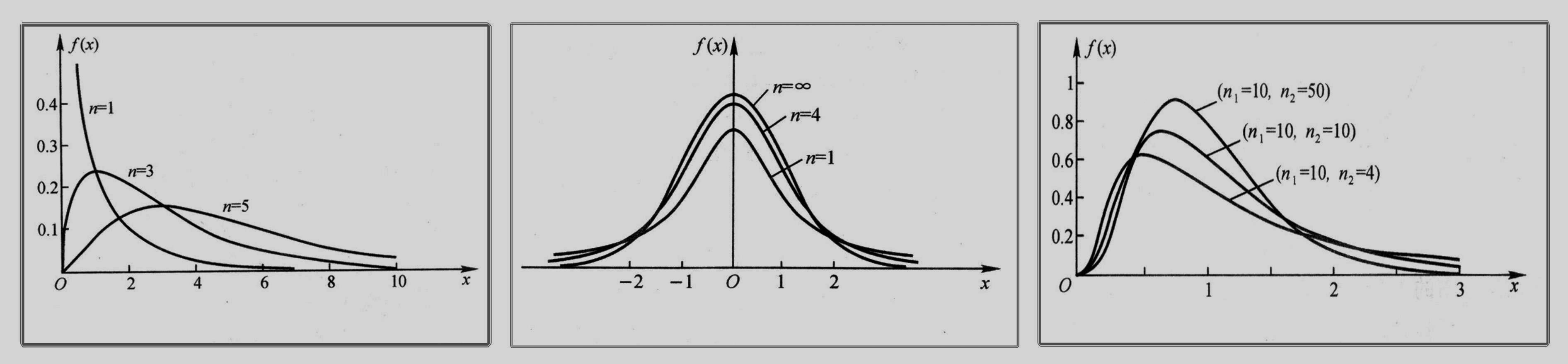
上述三种分布的密度函数曲线依次如图
(3)分位数
设 $X\sim\Psi(n)$,$\Psi$ 是某种分布,$n$ 相应的自由度,$0<\alpha<1$,称满足 $P(X\leq\Psi_\alpha(n))=\alpha$ 的数为分布 $\Psi(n)$ 的 $\alpha$ 分位数(或分位点)。相当于求 $\alpha$ 点的密度函数积分。
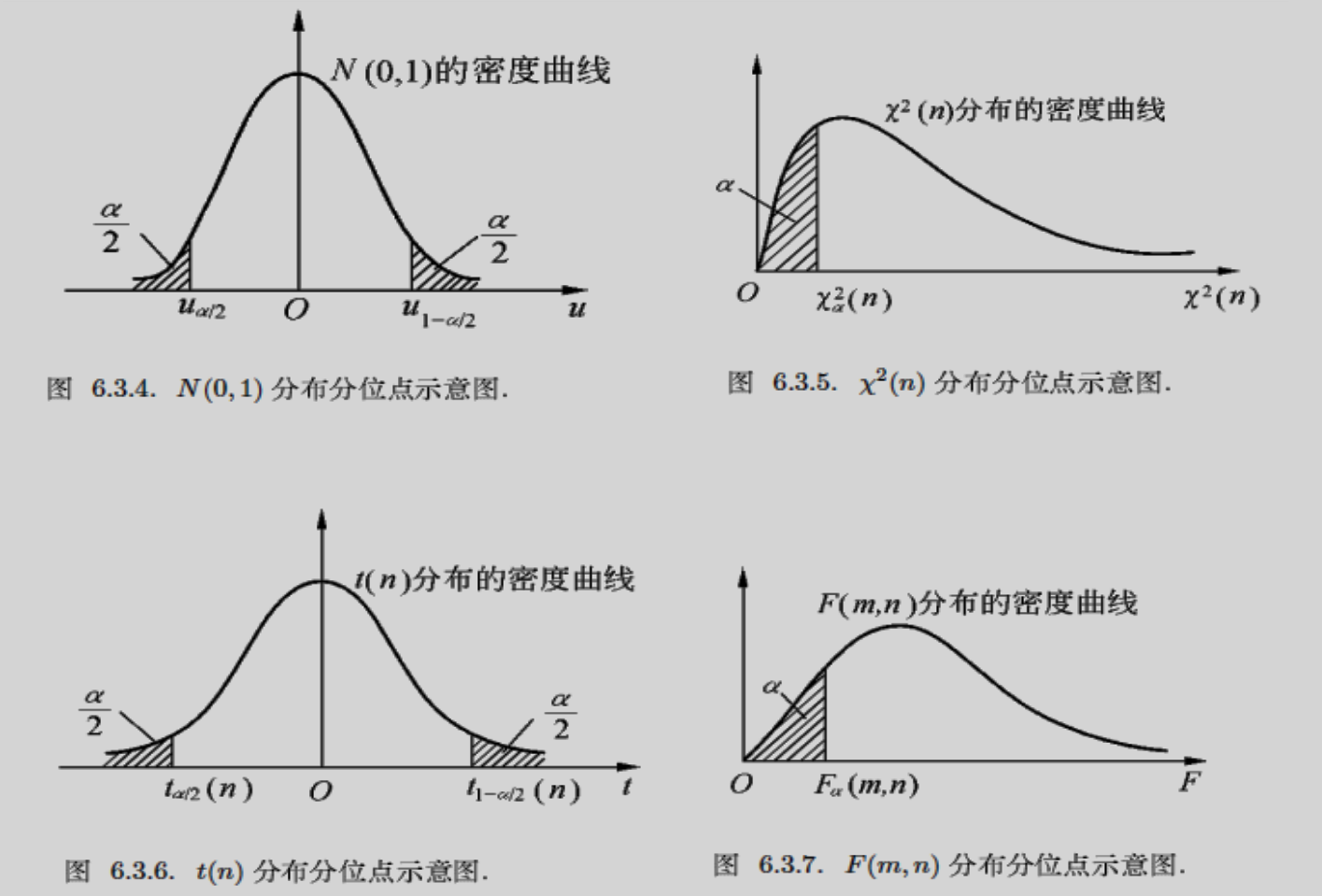
四大分布的分位数示意图
(4)正态总体的抽样分布
定理 1(单个正态总体下的抽样分布) 设 $X_1,X_2,…,X_n$ 是来自正态总体 $N(\mu,\sigma^2)$ 的一个样本,则有样本均值 $\overline{X}$ 与样本方差 $S_n^2$ 相互独立,且:
\[\overline{X}\sim{N(\mu,\frac{\sigma^2}{n})}\] \[\frac{nS_n^2}{\sigma^2}=\frac{\sum_{i=1}^{n}(X_i-\overline{X})^2}{\sigma^2}\sim\chi^2(n-1)\]根据定理有以下推论:
- 当总体为标准正态分布时,有 $\overline{X}\sim{N(0,\frac{1}{n})},\ nS_n^2\sim\chi^2(n-1)$
- $\mu$ 为总体均值,有:
定理 2(两个正态总体下的抽样分布) 设总体 $X,Y$ 相互独立 $X_1,X_2,…,X_m$ 是来自正态总体 $N(\mu_1,\sigma_1^2)$ 的一个样本,$Y_1,Y_2,…,Y_n$ 是来自正态总体 $N(\mu_2,\sigma_2^2)$ 的一个样本,则有以下结论:
\[\frac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{\sqrt{\sigma_1^2/m+\sigma_2^2/n}}\sim{N(0,1)}\] \[F=\frac{mS_{1m}^2}{nS_{2n}^2}\cdot\frac{\sigma_2^2}{\sigma_1^2}\cdot\frac{n-1}{m-1}= \frac{mS_{1m}^{*2}}{nS_{2n}^{*2}}\cdot\frac{\sigma_2^2}{\sigma_1^2}\sim{F(m-1,n-1)}\] \[F=\frac{n\sum_{i=1}^{m}(X_i-\mu_1)^2}{m\sum_{j=1}^{n}(Y_j-\mu_2)^2} \cdot\frac{\sigma_2^2}{\sigma_1^2}\sim{F(m,n)}\]另外当 $X,Y$ 所在总体的方差同为 $\sigma$ 时,有:
\[\frac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{S_\omega\sqrt{\frac{1}{m}+\frac{1}{n}}}\sim{t(m+n-2)}\]其中:
\[S_\omega^2=\frac{(m-1)S_{1m}^{*2}+(n-1)S_{2n}^{*2}}{m+n-2}\]CHPT07 – 参数估计
已知总体分布类型,估计分布参数
一、点估计
构造一个统计量 $\widehat{\theta}$ 对参数 $\theta$ 进行定值的估计称为参数的点估计。
概率函数:对于离散型,概率函数 $f(x)=P{X=x}$;对于连续型,概率函数即密度函数。
(1)矩法估计
据估计的想法源自大数定理。如果总体 $X$ 存在 $k$ 阶矩,对任意 $\varepsilon>0$ 有:
\[\lim_{n\rightarrow\infty}P\left(\bigg|\frac{1}{n}\sum_{i=1}^{n}X_i^k-EX^k\bigg|\geq\varepsilon\right)=0\]即当样本容量足够大时,矩法估计的参数与总体参数差别很小。即,可直接用样本的 $k$ 阶矩近似总体的 $k$ 阶矩。
(2)最大似然估计法
定义:总体 $X$ 的概率函数为 $f(x,\theta)$,$\theta$ 为未知参数。$x_1,x_2,…,x_n$ 是取自总体 $X$ 的一组样本观测值,如 $\theta=\widehat\theta$ 时,$x_1,x_2,…,x_n$ 被取到的概率最大(即似然函数 $L$ 取到最大值),则称 $\widehat\theta$ 为 $\theta$ 的最大似然估计。即,最大似然估计值就是最可能产生观测值 $x_1,x_2,…,x_n$ 的参数值。
具体步骤:
a) 列出似然函数 $L(x_1,x_2,…,x_n,\theta)$
当总体为离散型分布时,其分布律写为:$P(X=x_i)=p(x_i,\theta),\ i=1,2,…,n$。对给定的样本观测值 $x_1,x_2,…,x_n$,令:
\[L(x_1,x_2,...,x_n,\theta)=\prod_{i=1}^{n}p(x_i,\theta)\]当总体为连续型分布是,密度函数写为:$f(x,\theta)$。对给定的样本观测值 $x_1,x_2,…,x_n$,令:
\[L(x_1,x_2,...,x_n,\theta)=\prod_{i=1}^{n}f(x_i,\theta)\]b)求似然函数的极值点 $\widehat\theta$
最大似然估计法的前提是似然函数关于 $\theta$ 可微。则最大值点 $\widehat\theta$ 满足方程:
\[\frac{dL(x_1,x_2,...,x_n,\theta)}{d\theta}=0\]求得的 $\widehat\theta$ 即为 $\theta$ 的最大似然估计。又由于 $L$ 为连乘形式,则 $\ln{x}$ 是 $x$ 的单调函数,所以可以简化微分的求解:$\frac{d\ln{L}}{d\theta}=0$。更一般的情况,若有多个未知参数,其似然函数为 $L(x_1,x_2,…,x_n,\theta_1,\theta_2,…\theta_m)$,可通过偏微分一一求解每个参数的最大似然估计:
\[\frac{\partial\ln{L}}{\partial\theta_j}=0\Rightarrow\widehat\theta_j,\ \ \ \ j=1,2,...,m\]二、衡量估计量的优劣性
(1)无偏估计
设总体 $X\sim{F_X(\cdot,\theta)},\ \theta\in\Theta$,统计量 $T(X_1,X_2,…,X_n)$ 为 $g(\theta)$ 的估计量。如果 $ET=g(\theta)$,则称 $T(X_1,X_2,…,X_n)$ 为 $g(\theta)$ 的无偏估计量。如果 $\lim_{n\rightarrow\infty}ET=g(\theta)$,则称 $T(X_1,X_2,…,X_n)$ 为 $g(\theta)$ 的渐进无偏估计量。
无偏估计的意义是,虽然统计量由于随机性而偏离总体的真值,但其数学期望等于真值,没有系统偏差。
(2)一致最小方差无偏估计
设总体 $X\sim{F_X(\cdot,\theta)},\ \theta\in\Theta$,统计量 $T_0(X_1,X_2,…,X_n)$ 为 $g(\theta)$ 的无偏估计量,且对 $g(\theta)$ 的任意无偏估计量 $T(X_1,X_2,…,X_n)$ 都有 $Var[T_0]\leq{Var[T]}$,则称 $T_0$ 为 $g(\theta)$ 的一致最小方差无偏估计量。
(3)一致估计
设总体 $X\sim{F_X(\cdot,\theta)},\ \theta\in\Theta$,统计量 $T(X_1,X_2,…,X_n)$ 为 $g(\theta)$ 的估计量。如对于任意 $\varepsilon>0$ 有 $\lim_{n\rightarrow\infty}P(|T-g(\theta)|\geq\varepsilon)=1$,则称 $T(X_1,X_2,…,X_n)$ 是 $g(\theta)$ 的一致估计量或相合估计量。样本均值 $\overline{X}$ 是总体均值 $\mu$ 的一致估计量,修正样本方差 $S_n^{*2}$ 是总体方差 $\sigma^2$ 的一致估计量。
三、区间估计
定义:设总体 $X\sim{F_X(\cdot,\theta)},\ \theta\in\Theta$,$g$ 为 $\theta$ 的函数。如有统计量 $T_1(X_1,X_2,…,X_n)$ 和 $T_2(X_1,X_2,…,X_n)$ 使得对给定的 $\alpha\ (0<\alpha<1)$ 有 $P(T_1\leq{g(\theta)}\leq{T_2})=1-\alpha$,则随机区间 $[T_1,T_2]$ 称为参数 $g(\theta)$ 的置信度为 $1-\alpha$ 的置信区间。即,随机区间 $[T_1,T_2]$ 中包含 $g(\theta)$ 的概率为 $1-\alpha$。
(1)单个正态总体的区间估计
a)已知 $\sigma$,求 $\mu$ 的置信区间
由定理,若 $\overline{X}\sim{N(\mu,\sigma^2/n)}$,则:
\[U=\frac{\overline{X}-\mu}{\sqrt{\sigma^2/n}}\sim{N(0,1)}\]对于给定的置信度 $1-\alpha$,根据标准正态分布的分位数,有:
\[P\left(\bigg|\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\bigg|<U_{1-\frac{\alpha}{2}}\right)=1-\alpha\\ \Rightarrow P\left(-U_{1-\frac{\alpha}{2}}<\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}<U_{1-\frac{\alpha}{2}}\right)\\ \Rightarrow P\left(\overline{X}-U_{1-\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}<\mu<\overline{X}+U_{1-\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}\right)=1-\alpha\]故 $\mu$ 的置信区间为:
\[\left[\overline{X}-U_{1-\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}},\ \overline{X}+U_{1-\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}\right]\]b)未知 $\sigma$,求 $\mu$ 的置信区间
使用样本方差 $S_n^2$ 代替总体方差构造统计量:
\[t=\frac{\overline{X}-\mu}{S_n/\sqrt{n-1}}=\frac{(\overline{X}-\mu)\sqrt{n-1}}{S_n}\sim{t(n-1)}\]对于给定的置信度 $1-\alpha$,根据 $t$ 分布的分位数,有:
\[P\left(\bigg|\frac{\overline{X}-\mu}{S_n/\sqrt{n-1}}\bigg|<t_{1-\frac{\alpha}{2}}(n-1)\right)=1-\alpha\]故 $\mu$ 的置信区间为:
\[\left[\overline{X}-t_{1-\frac{\alpha}{2}}(n-1)\frac{S_n}{\sqrt{n-1}},\ \overline{X}+U_{1-\frac{\alpha}{2}}(n-1)\frac{S_n}{\sqrt{n-1}}\right]\]c)已知 $\mu$,求 $\sigma^2$ 的置信区间
使用 $\mu$ 构造统计量:
\[\chi^2=\sum_{i=1}^{n}\frac{(X_i-\mu)^2}{\sigma^2}\sim\chi^2(n)\]对于给定的置信度 $1-\alpha$,根据 $\chi^2$ 分布的分位数,有:
\[P\left(\chi^2_\frac{\alpha}{2}(n)<\sum_{i=1}^{n}\frac{(X_i-\mu)^2}{\sigma^2}<\chi^2_{1-\frac{\alpha}{2}}(n)\right)\]求得 $\sigma^2$ 的置信区间为:
\[\left[\frac{\sum_{i=1}^{n}(X_i-\mu)^2}{\chi^2_{1-\frac{\alpha}{2}(n)}},\ \frac{\sum_{i=1}^{n}(X_i-\mu)^2}{\chi^2_\frac{\alpha}{2}(n)}\right]\]d)未知 $\mu$,求 $\sigma^2$ 的置信区间
使用 $\overline{X}$ 构造统计量:
\[\chi^2=\sum_{i=1}^{n}\frac{(X_i-\overline{X})^2}{\sigma^2}=\frac{nS_n^2}{\sigma^2}\sim\chi^2(n-1)\]对于给定的置信度 $1-\alpha$,根据 $\chi^2$ 分布的分位数,有:
\[P\left(\chi^2_\frac{\alpha}{2}(n-1)<\sum_{i=1}^{n}\frac{(X_i-\overline{X})^2}{\sigma^2}<\chi^2_{1-\frac{\alpha}{2}}(n-1)\right)\]求得 $\sigma^2$ 的置信区间为:
\[\left[\frac{nS_n^2}{\chi^2_{1-\frac{\alpha}{2}(n-1)}},\ \frac{nS_n^2}{\chi^2_\frac{\alpha}{2}(n-1)}\right]\](2)两个正态总体的区间估计
a)$\sigma_1^2,\sigma_2^2$ 已知,求 $\mu_1-\mu_2$ 的置信区间
构造统计量:
\[u=\frac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}}}\sim{N(0,1)}\]对于给定的置信度 $1-\alpha$,根据标准正态分布分布的分位数,有:
\[P\left(\Bigg\vert\frac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}}}\Bigg\vert<u_{1-\frac{\alpha}{2}}\right)=1-\alpha\]求得 $\mu_1-\mu_2$ 的置信区间为:
\[\left[(\overline{X}-\overline{Y})-u_{1-\frac{\alpha}{2}}\sqrt{\frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}},\ (\overline{X}-\overline{Y})+u_{1-\frac{\alpha}{2}}\sqrt{\frac{\sigma_1^2}{m}+\frac{\sigma_2^2}{n}}\right]\]b)$\sigma_1^2,\sigma_2^2$ 未知(已知 $\sigma_1^2=\sigma_2^2$ ),求 $\mu_1-\mu_2$ 的置信区间
构造统计量:
\[t=\frac{(\overline{X}-\overline{Y})-(\mu_1-\mu_2)}{S_\omega\sqrt{\frac{1}{m}+\frac{1}{n}}}\sim{t(m+n-2)}\]其中:
\[S_\omega^2=\frac{(m-1)S_{1m}^{*2}+(n-1)S_{2n}^{*2}}{m+n-2}==\frac{mS_{1m}^{2}+nS_{2n}^{2}}{m+n-2}\]对于给定的置信度 $1-\alpha$,根据标准 $t$ 分布的分位数,求得 $\mu_1-\mu_2$ 的置信区间为:
\[\left[(\overline{X}-\overline{Y})-t_{1-\frac{\alpha}{2}}(m+n-2)S_\omega\sqrt{\frac{1}{m}+\frac{1}{n}},\ (\overline{X}-\overline{Y})+t_{1-\frac{\alpha}{2}}(m+n-2)S_\omega\sqrt{\frac{1}{m}+\frac{1}{n}}\right]\]c)$\mu_1,\mu_2$ 已知,求 $\sigma_1^2/\sigma_2^2$ 的置信区间
构造统计量:
\[F=\frac{\frac{1}{m\sigma_1^2}\sum_{i=1}^{m}(X_i-\mu_1)^2}{\frac{1}{n\sigma_2^2}\sum_{j=1}^{n}(Y_j-\mu_2)^2}\sim{F(m,n)}\]对于给定的置信度 $1-\alpha$,根据 $F$ 分布的分位数,有:
\[P\left(F_\frac{\alpha}{2}(m,n)<F<F_{1-\frac{\alpha}{2}}(m,n)\right)=1-\alpha\]求得 $\sigma_1^2/\sigma_2^2$ 的置信区间为:
\[\left[\frac{1}{F_{1-\frac{\alpha}{2}}(m,n)}\frac{n\sum_{i=1}^{m}(X_i-\mu_1)^2}{m\sum_{j=1}^{n}(Y_j-\mu_2)^2},\ \frac{1}{F_\frac{\alpha}{2}(m,n)}\frac{n\sum_{i=1}^{m}(X_i-\mu_1)^2}{m\sum_{j=1}^{n}(Y_j-\mu_2)^2}\right]\]d)$\mu_1,\mu_2$ 未知,求 $\sigma_1^2/\sigma_2^2$ 的置信区间
构造统计量:
\[F=\frac{\frac{1}{(m-1)\sigma_1^2}\sum_{i=1}^{m}(X_i-\overline{X})^2}{\frac{1}{(n-1)\sigma_2^2}\sum_{j=1}^{n}(Y_j-\overline{X})^2} =\frac{S_{1m}^{*2}/\sigma_1^2}{S_{2n}^{*2}/\sigma_2^2}\sim{F(m-1,n-1)}\]对于给定的置信度 $1-\alpha$,根据 $F$ 分布的分位数,求得 $\sigma_1^2/\sigma_2^2$ 的置信区间为:
\[\left[\frac{1}{F_{1-\frac{\alpha}{2}}(m-1,n-1)}\frac{(n-1)\sum_{i=1}^{m}(X_i-\overline{X})^2}{(m-1)\sum_{j=1}^{n}(Y_j-\overline{Y})^2},\ \frac{1}{F_\frac{\alpha}{2}(m-1,n-1)}\frac{(n-1)\sum_{i=1}^{m}(X_i-\overline{X})^2}{(m-1)\sum_{j=1}^{n}(Y_j-\overline{Y})^2}\right]\]代入修正样本方差,写为:
\[\left[\frac{1}{F_{1-\frac{\alpha}{2}}(m-1,n-1)}\frac{S_{1m}^{*2}}{S_{2n}^{*2}},\ \frac{1}{F_\frac{\alpha}{2}(m-1,n-1)}\frac{S_{1m}^{*2}}{S_{2n}^{*2}}\right]\](3)单个正态总体参数的联合区间估计
由上一章的抽样分布的样本均值和样本方差有:
\[\frac{\overline{X}-\mu}{\sqrt{\sigma^2/n}}\sim{N(0,1)},\ \ \ \ \frac{nS_n^2}{\sigma^2}\sim\chi^2(n-1)\]联合置信概率写为:
\[P\left(\frac{\overline{X}-\mu}{\sqrt{\sigma^2/n}}\leq{I},\ k_1\leq\frac{nS_n^2}{\sigma^2}\leq{k_2}\right)=1-\alpha\]由于 $\overline{X}$ 与 $S_n^2$ 相互独立,有:
\[P\left(\frac{\overline{X}-\mu}{\sqrt{\sigma^2/n}}\leq{I}\right)\cdot{P}\left(k_1\leq\frac{nS_n^2}{\sigma^2}\leq{k_2}\right)=1-\alpha\] \[\Rightarrow P\left(\bigg|\frac{\overline{X}-\mu}{\sqrt{\sigma^2/n}}\bigg|\leq{I}\right)=\sqrt{1-\alpha},\ P\left(k_1\leq\frac{nS_n^2}{\sigma^2}\leq{k_2}\right)=\sqrt{1-\alpha}\] \[\Rightarrow P\left(\frac{n(\overline{X}-\mu)^2}{I^2}\leq{\sigma^2}\right)=\sqrt{1-\alpha},\ P\left(\frac{nS_n^2}{k_2}\leq\sigma^2\leq{\frac{nS_n^2}{k_1}}\right)=\sqrt{1-\alpha}\]由:
\[I=u_\frac{1+\sqrt{1-\alpha}}{2},\ k_1=\chi^2_\frac{1-\sqrt{1-\alpha}}{2}(n-1),\ k_2=\chi^2_\frac{1+\sqrt{1-\alpha}}{2}(n-1)\]求得 $(\mu,\sigma^2)$ 的联合置信区间为:
\[\left\{(\mu,\sigma^2):\ \frac{n(\overline{X}-\mu)^2}{u^2_\frac{1+\sqrt{1-\alpha}}{2}}\leq\sigma^2,\ \frac{nS_n^2}{\chi^2_\frac{1+\sqrt{1-\alpha}}{2}(n-1)}\leq\sigma^2\leq{\frac{nS_n^2}{\chi^2_\frac{1-\sqrt{1-\alpha}}{2}(n-1)}}\right\}\](4)非正态总体参数的区间估计
设总体 $X\sim{F_X(\cdot,\theta)}$,当样本容量 $n\rightarrow\infty$,近似有:
\[\sqrt{n}\cdot\frac{\overline{X}-EX}{S_n}\sim{N(0,1)}\]CHPT08 – 假设检验
一、假设检验与两类错误
(1)假设检验的提法
- 提出原假设 $H_0$ 与备选假设(对立假设)$H_1$
- 确定统计量 $T(X_1,X_2,…,X_n)$、显著性水平 $\alpha$、临界值 $k$,按下式进行抽样检验:
- 满足 $T(X_1,X_2,…,X_n)\geq{k}$ 时,拒绝 $H_0$,反之接受 $H_0$
(2)假设检验的两类错误
第一类错误:拒真错误 – $H_0$ 正确,但是拒绝了 $H_0$:$\alpha=P(拒绝H_0|H_0真)$
第二类错误:受伪错误 – $H_0$ 不正确,但是接受了 $H_0$:$\beta=P(接受H_0|H_0伪)$
- $\beta\neq{1-\alpha}$
- 样本量一定时,不可能同时缩小两类错误的概率;$\alpha$ 变小时,$\beta$ 变大
- 现实中样本容量有限,一般在控制 $\beta$ 不超过某个值的前提下,尽可能缩小 $\alpha$
- 实际中常用的方法是只控制 $\alpha$ 的检验方法,称为显著性检验;当想用显著性检验对某一猜测进行强有力的支持时,应将该猜测的对立命题作为原假设 $H_0$
二、正态总体参数的假设检验
(1)单个正态总体的假设检验
已知 $\sigma^2$,$H_0:\ \mu=\mu_0\ \ \ \ H_1:\ \mu\neq\mu_0$
- 提出假设:$H_0:\ \mu=\mu_0$
- 确定样本函数的统计量:$u=\frac{\overline{X}-\mu_0}{\sigma/\sqrt{n}}\sim{N(0,1)}$
- 给定显著性水平 $\alpha$,根据正态分布函数得到临界值 $k=u_{1-\frac{\alpha}{2}}$,令
- 根据给定样本求出统计量 $u$ 的观测值 $u_1$
- 若 $|u_1|<k$ 则接受 $H_0$,反之拒绝 $H_1$
重点在于统计量的选择,另外还有三种情况,实际上与置信区间的推导过程一一对应。此处省略过程,总结为下表:

注:表中列出的为拒绝域
(2)两个正态总体的假设检验
已知 $\sigma_1^2,\ \sigma_2^2$,$H_0:\ \mu_1-\mu_2=\delta\ \ \ \ H_1:\ \mu_1-\mu_2\neq\delta$
- 提出假设:$H_0:\ \mu_1-\mu_2=\delta$
- 确定样本函数的统计量:
- 给定显著性水平 $\alpha$,根据正态分布函数得到临界值 $k=u_{1-\frac{\alpha}{2}}$,令
- 根据给定样本求出统计量 $u$ 的观测值 $u_1$
- 若 $|u_1|<k$ 则接受 $H_0$,反之拒绝 $H_1$
重点在于统计量的选择,另外还有三种情况,实际上与置信区间的推导过程一一对应。此处省略过程,总结为下表:

注:表中列出的为拒绝域
三、非正态总体均值的假设检验
单个总体 $X$ 的均值 $EX$ 的假设检验问题:
- $H_0:\ EX=\mu_0\ (或\leq\mu_0,\ 或\geq\mu_0)$
- $H_1:\ EX\neq\mu_0\ (或>\mu_0,\ 或<\mu_0)$
当方差 $Var[X]$ 已知,$n\rightarrow\infty$ 时,近似有:
\[\frac{\overline{X}-EX}{\sqrt{Var[X]/n}}\sim{N(0,1)}\]当方差 $Var[X]$ 未知,$n\rightarrow\infty$ 时,近似有:
\[\frac{\overline{X}-EX}{\sqrt{S_n^2/n}}\sim{N(0,1)}\]两个个总体 $X,Y$ 的均值差 $EX-EY$ 的假设检验问题:
- $H_0:\ EX-EY=\delta\ (或\leq\delta,\ 或\geq\delta)$
- $H_1:\ EX-EY\neq\delta\ (或>\delta,\ 或<\delta)$
当方差 $Var[X],Var[Y]$ 已知,$m,n\rightarrow\infty$ 时,近似有:
\[\frac{(\overline{X}-\overline{Y})-(EX-EY)}{\sqrt{Var[X]/m+Var[Y]/n}}\sim{N(0,1)}\]当方差 $Var[X],Var[Y]$ 未知,$m,n\rightarrow\infty$ 时,近似有:
\[\frac{(\overline{X}-\overline{Y})-(EX-EY)}{\sqrt{S_{1m}^2/m+S_{2n}^2/n}}\sim{N(0,1)}\]四、非参数假设检验
非参数假设检验适用于不确定总体分布的情况。研究的检验是如何用样本去拟合总体的分布,又称为分布的拟合优度检验。一般有两种思路:
- 拟合总体的分布函数
- 拟合总体的概率函数
常用的总体分布假设检验方法:$\chi^2$—拟合优度检验。