“A/B 测试的概念来源于生物医学的双盲测试,双盲测试中病人被随机分成两组,在不知情的情况下分别给予安慰剂和测试用药,经过一段时间的实验后再来比较这两组病人的表现是否具有显著的差异,从而决定测试用药是否真的有效。”
一、A/B 测试简介
简单理解,就是在进行客户端或运营策略等更改时,向不同用户呈现不同的版本,以确定有利的更改方式。
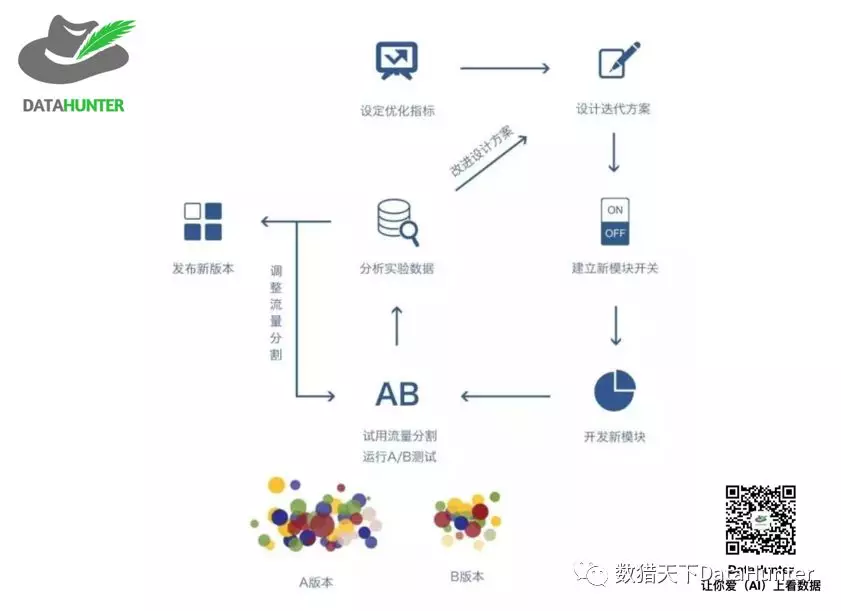
测试基本流程:
- (1) 从业务的角度确定改进的点 —— 一般应用场景有:
- APP、网页、小程序等的用户体验优化
- 后端算法,如推荐算法、广告算法,的优化
- (2) 设定衡量优劣的指标 —— 根据实际应用确定相关指标:
- 流程优化:转化率
- 用户激活:购买率
- 推荐算法优化:点击率
- (3) 开发测试的版本
- (4) 确定测试时长、分流方案
- 开始时间应该避开访问量高峰,如节假日、促销活动、每日的访问高峰期,等
- 总时长不应太短,避免用户分布产生偏差、受“新奇效应”影响、样本量不够,等
- 分流时确保样本量大小足够,并且考虑转化率导致特定环节的用户减少
- 分流应考虑用户特征,分层抽样,控制变量
- (5) 部署测试,收集数据,分析结果
- (6) 根据结果确定下一步
- a) 发布新版本
- b) 调整方案重新测试
- c) 回到 (1) 测试下一个改进点
二、假设检验简介
假设,在 A/B 测试中,我们开发了两个版本。一个是包含蓝色的“添加购物车”按钮,产生了 100 万元的购买;另一个是红色的“添加购物车”按钮,产生了 1000 万元的购买。那我们可以自信地说:“红色的按钮更好”。但是如果另一个是 200 万元、110 万元,或者 101 万元呢?那就可能只是分流时产生的随机差异。所以假设检验解决的问题就是:到底差异多大时才是显著的?或者换句话说,要有多大的差异才能支撑我们自信地得出结论。
在 (5) 中分析结果时使用假设检验方法。关于假设检验的基础知识和流程,以及背后的统计学原理,可以参考这里。

主要需要考虑两个问题,一个是显著性水平(决定了接受或推翻假设),另一个是总体的先验分布(决定了使用的统计量)。一般来说,显著性水平是根据业务需要设定的,一般可以取 0.01、0.05、0.1。统计量根据总体分布和样本量确定:
- 对于正态总体,已知总体方差,使用 Z 检验(U 检验);反之使用 T 检验
- 对于非正态总体,如果样本容量足够大,可以利用中心极限定理
- 对于小样本非正态总体参数估计,可以参考这篇文章
- 对于更复杂的情况,例如多个分组的问题,可以使用方差分析,详见这篇文章
三、案例实践
案例参考知乎文章:一文入门 A/B 测试(含流程、原理及示例)。更详细实例待更新…
引用 & 鸣谢
A/B Testing Measurement Frameworks
Hypothesis Testing – What it is and how to do it in Python
待续