一、简介
前面的文章中通过假设对比来检验样本是否服从泊松分布。得出的结论是总体分布不服从泊松分布,那么如何找到与总体分布最接近的分布呢?不可能一个个分布去验证。这里便可以用到 fitter 这个库。
fitter 是一个很小的第三方库,提供了一个简单的类来拟合数据的分布,亦即找出与样本最接近的理想的分布。
二、安装
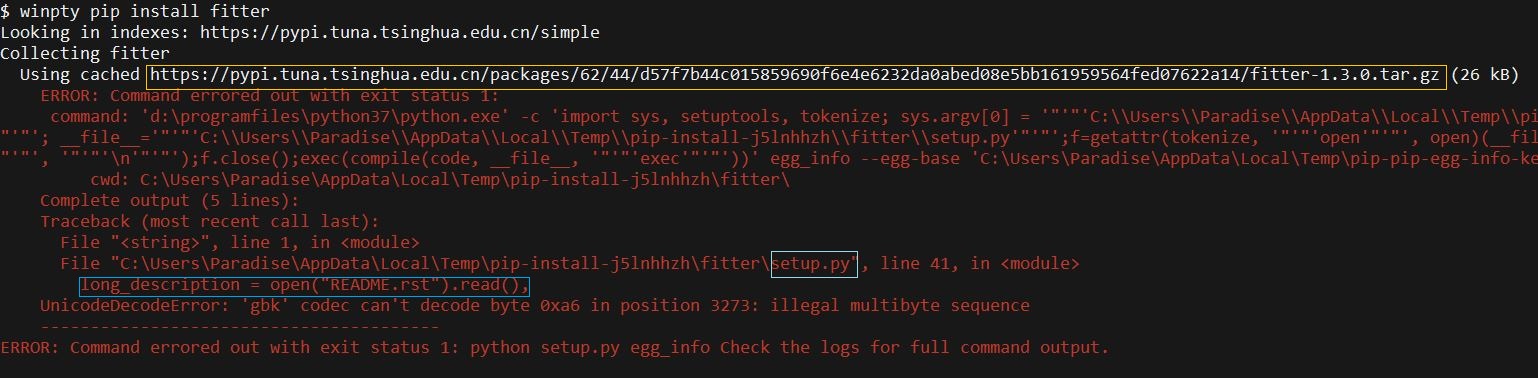
首先安装 fitter,通过 pip install fitter 安装时(v1.3.0),可能会产生报错如下图。根据报错信息(蓝色框部分)可以知道是由于编码问题导致读取文档时出错。因此可以通过在 setup.py 的代码中指定编码来解决。首先通过在浏览器打开下图中的链接,即可下载该库的压缩包到本地。然后将其解压,更改 setup.py 中报错的代码为:long_description = open("README.rst", encoding="utf-8").read(),。最后可以直接在该目录下运行 setup.py 完成安装:python setup.py build,python setup.py install。
三、测试
还是前面的文章中用到的订单数据,这里先简单的进行分组聚合计算用户购买次数,然后使用 fitter 拟合总体的分布。
1
2
3
4
5
6
7
8
9
import pandas as pd
from scipy import stats
from fitter import Fitter
df = pd.read_csv('orders.csv')
rv = df.groupby('customerId').count().values.reshape(len(df.customerId.unique()), )
f = Fitter(rv)
f.fit() # 这里会运行相当长的一段时间,默认拟合 stats 子模块中所有的分布类型
f.summary()
1
2
3
4
5
6
7
8
In [4]: f.summary()
Out[4]:
sumsquare_error aic bic kl_div
mielke 0.059989 1175.240085 -7278.518586 inf
burr 0.059989 1175.241738 -7278.518411 inf
burr12 0.060060 1219.259660 -7277.604984 inf
f 0.060206 1238.451482 -7275.721995 inf
betaprime 0.060206 1238.451445 -7275.721993 inf
上面结果的 aic,bic 分别是修正信息标准和贝叶斯信息标准,信息标准(Information criterion)是用于模型选择的一个指标,比较两个模型时,信息标准越低越好。而 kl_div(Kullback Leibler Divergence)为相对熵或称信息散度,相对熵表示使用理论分布拟合真实分布时产生的信息损耗。查看文档中的源码可以看到这几个值在 Fitter._fit_single_distribution 这个类方法中定义和计算。
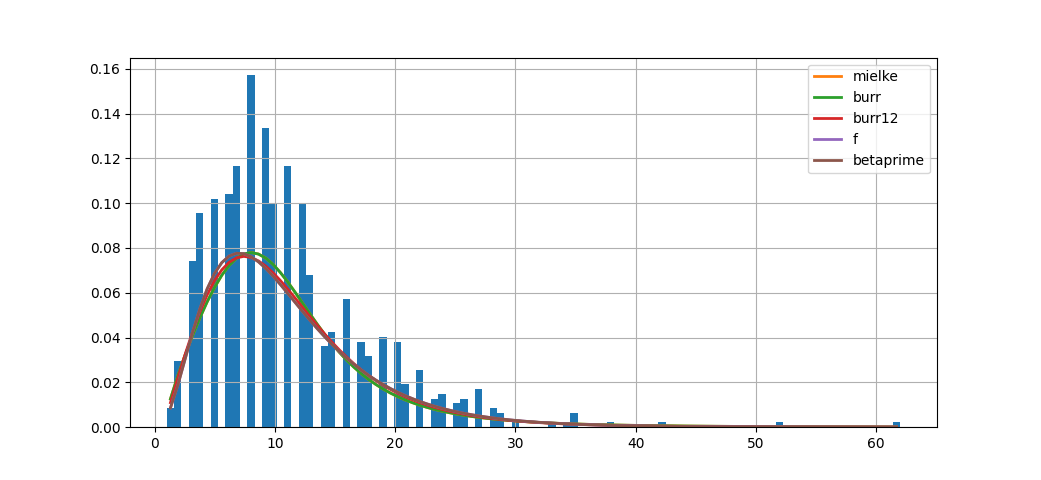
为了减少运行时间,下面只测试 10 个常见的分布类型。结果耗时大大缩短,但是结果也不如前者更准确。
1
2
3
4
import fitter
f = Fitter(data, distributions=fitter.get_common_distributions())
f.fit()
f.summary()
1
2
3
4
5
6
7
8
In [10]: f.summary()
Out[10]:
sumsquare_error aic bic kl_div
lognorm 0.060282 1220.340678 -7281.397879 inf
chi2 0.060321 1315.115666 -7280.908214 inf
gamma 0.060321 1315.107754 -7280.907903 inf
rayleigh 0.063585 1774.082387 -7246.870226 inf
cauchy 0.065384 1147.192894 -7225.327891 inf
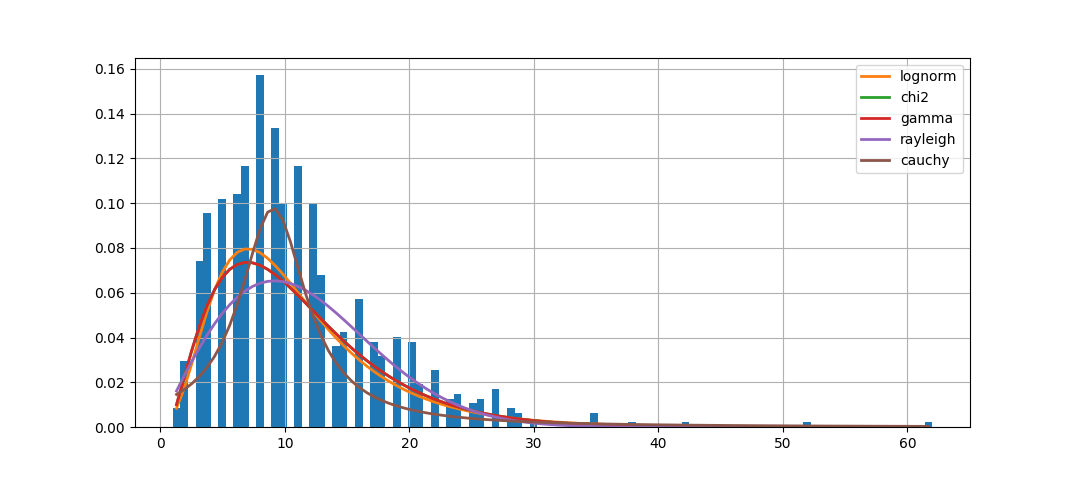
最终得到的结果是,购买次数的分布最接近于 mielke 分布(但是实际上,根据上述对拟合指标的分析,拟合效果是较差的,所以这里仅仅作为一种参考)。总的来说,在实际问题中,随机变量的分布是比理论模型复杂得多的,并且可能是一直在变动而没有一个固定的分布的。因此除了需要更多的数据,还需要控制各种变量才能得到一个确定的总体的总体分布。